Work

Sponsored Links

When a body is moved as a result of a force being applied to it, work is done.

The amount of work is the product of the applied force and the distance:

W = F s         (1)

where

W = work done (J, ft lb)

F = force acting on the object (N, lb)

s = distance object moved in the direction of the force (m, ft)

The unit of work is joule, J, which is defined as the amount of work done when a force of 1 Newton acts for distance of 1 m in the direction of the force.

• 1 J (Joule) = 0,1020 kpm = 2.778x10^-7 kWh = 2.389x10^-4 kcal = 0.7376 ft lb_f = 1 (kg m²)/s² = 1 watt second = 1 Nm = 1 ft lb = 9.478x10^-4 Btu
• 1 ft lb_f (foot pound force) = 1.3558 J = 0.1383 kp m = 3.766x10^-7 kWh = 3.238x10^-4 kcal = 1.285x10^-3 Btu

This is the same unit as energy.

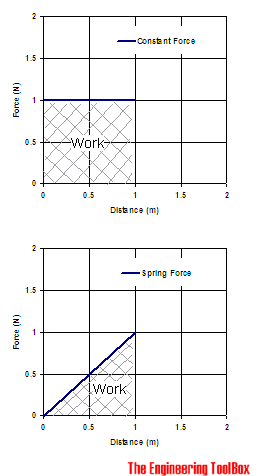
The work done by a constant force and a spring force can be visualized as the area under the graph in distance force diagrams like

Example - Constant Force

A constant force of 20 N is acting a distance of 30 m. The work done can be calculated as

W = (20 N) (30 m)

    = 60 (J, Nm)

Example - Spring Force

A spring is extended 40 mm by a force of 20 N. The work done can be calculated as

W = 1/2 (20 N) (0.040 m)

    = 0.4 (J, Nm)

Example - Climbing Stairs, Imperial units

The work made by a person of 150 lb climbing a stair of 100 ft can be calculated as

W = (150 lb) (100 ft)

    = 15,000 ft lb

Sponsored Links

Related Topics

• Dynamics - Dynamics Motion - velocity and acceleration
• Mechanics - Kinematics, forces, vectors, motion, momentum, energy and the dynamics of objects
• Thermodynamics - The effects of work, heat and energy on a system

Related Documents

• 1st Law of Thermodynamics - The First Law of Thermodynamics simply states that energy can be neither created nor destroyed (conservation of energy). Thus power generation processes and energy sources actually involve conversion of energy from one form to another, rather than creation of energy from nothing
• Energy - Energy is the capacity to do work
• Force - Force, Newton's third Law and acceleration
• Heat, Work and Energy - Tutorial to heat, work and energy - essentials as specific heat and specific heat capacity
• Potential Energy - Elevation and potential energy
• Power - Power is a measure of the rate at which work is done or energy converted
• Specific Work of Turbo Machines - Pumps, Compressors and Fans - Specific work of pumps, fans, compressors and turbines