Hydraulic Force vs. Pascal's Law
Pascal's law and the hydraulic force acting in fluids.
Pascal's Laws relates to pressures in incompressible fluids - liquids.
- if the weight of a fluid is neglected the pressure throughout an enclosed volume will be the same
- the static pressure in a fluid acts equally in all directions
- the static pressure acts at right angles to any surface in contact with the fluid
Example - Pressure in a Hydraulic Cylinder
The pressure of 2000 Pa in an hydraulic cylinder acts equally on all surfaces. The force on a piston with area 0.1 m2 can be calculated
F = p A (1)
where
F = force (N)
p = pressure (Pa, N/m2)
A = area (m2)
or with values
F = (2000 Pa) (0.1 m2)
= 200 (N)
Example - Force in a Hydraulic Jack
The pressure acting on both pistons in a hydraulic jack is equal.
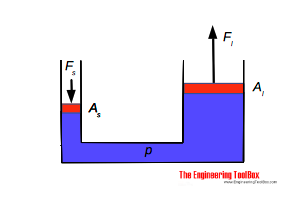
The force equation for the small cylinder:
Fs = p As (2)
where
Fs = force acting on the piston in the small cylinder (N)
As = area of small cylinder (m2)
p = pressure in small and large cylinder (Pa, N/m2)
The force equation for the large cylinder:
Fl = p Al (2b)
where
Fl = force acting on the piston in the large cylinder (N)
Al = area of large cylinder (m2)
p = pressure in small and large cylinder (Pa, N/m2)
(2) and (2b) can be combined to
Fs / As = Fl / Al (2c)
or
Fs = Fl As / Al (2d)
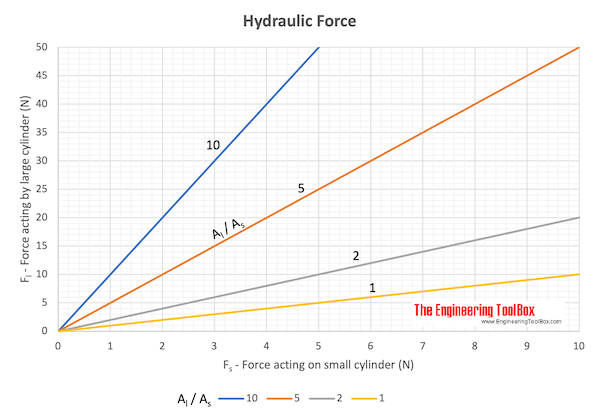
The equation indicates that the effort force required in the small cylinder to lift a load on the large cylinder depends on the area ratio between the small and the large cylinder - the effort force can be reduced by reducing the small cylinder area compared to the large cylinder area.
Related Mobile Apps from The Engineering ToolBox 
- free apps for offline use on mobile devices.
A Hydraulic Jack Lifting a Car
The back end (half the weight) of a car of mass 2000 kg is lifted by an hydraulic jack where the As / Al ratio is 0.1 (the area of the large cylinder is 10 times the area of the small cylinder).
The force - weight - acting on the large cylinder can be calculated with Newton's Second Law:
Fl = m a
where
m = mass (kg)
a = acceleration of gravity (m/s2)
or
Fl = 1/2 (2000 kg) (9.81 m/s2)
= 9810 (N)
The force acting on the small cylinder in the jack can be calculated with (2d)
Fs = (9810 N) 0.1
= 981 (N)
Related Topics
-
Fluid Mechanics
The study of fluids - liquids and gases. Involving velocity, pressure, density and temperature as functions of space and time. -
Gases and Compressed Air
Air, LNG, LPG and other common gas properties, pipeline capacities, sizing of relief valves.
Related Documents
-
Hydraulic Force vs. Pressure and Cylinder Size
Calculate hydraulic cylinder force. -
Hydrostatic Pressure vs. Depth
Depth and hydrostatic pressure. -
Pressure
Introduction to pressure - online pressure units converter.
