Liquids - Densities vs. Pressure and Temperature Change
Densities and specific volume of liquids vs. pressure and temperature change.
The density of a liquid will change with temperature and pressure. The density of water versus temperature and pressure is indicated below:
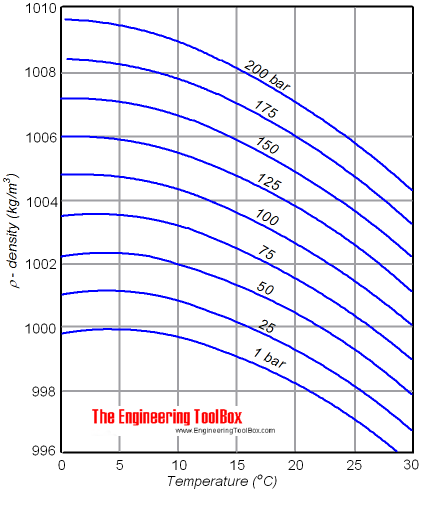
See also Water - Density, Specific Weight and Thermal Expantion Coefficient , for online calculator, figures and tables showing changes with temperature.
Density
The density of a liquid can be expressed as
ρ = m / V (1)
where
ρ = density of liquid (kg/m3 )
m = mass of the liquid (kg)
V = volume of the liquid (m3 )
The inverse of density is specific volume:
v = 1 / ρ
= V / m (2)
where
v = specific volume (m3 /kg)
Volume and change in Temperature
When temperature increases - most liquids expands:
dV = V1 - V0
= V0 β dt
= V0 β (t1 - t0 ) (3)
where
dV = V1 - V0 = change in volume - difference between final and initial volume (m3 )
β = volumetric temperature expansion coefficient (m3 /m 3 o C)
dt = t1 - t0 = change in temperature - difference between final and initial temperature (oC)
(3) can be modified to
V1 = V0 (1 + β (t1 - t0 )) (3b)
Density and change in Temperature
With (1) and (3b) the final density after a temperature change can be expressed as
ρ1 = m / ( V0 (1 + β (t1 - t0 ))) (4)
where
ρ1 = final density (kg/m3 )
- or combined with (2)
ρ1 = ρ0 / (1 + β (t1 - t0 )) (4b)
where
ρ0 = initial density (kg/m3 )
Volumetric Temperature Coefficients - β
- water : 0.0002 (m3 /m 3 o C) at 20 oC
- ethyl alcohol : 0.0011 (m3 /m 3 o C)
- volumetric expansion coefficient for some commonly used materials
Note! - volumetric temperature coefficients may vary strongly with temperature.
Density and change in Pressure
The influence of pressure on the volume of a liquid can be expressed with the three dimensional Hooke's law
E = - dp / (dV / V0 )
= - (p1 - p0 ) / ((V1 - V0 ) / V0 ) (5)
where
E = bulk modulus - liquid elasticity (N/m2)
The minus sign corresponds to the fact that an increase in the pressure leads to a decrease in volume.
With (5) - the final volume after pressure change can be expressed as
V1 = V0 (1 - (p1 - p0 ) / E) (5b)
Combining (5b) with (1) - the final density can be expressed as:
ρ1 = m / ( V0 (1 - (p1 - p0 ) / E)) (6)
- or combined with (2) - the final density can be expressed as
ρ1 = ρ0 / (1 - (p1 - p0 ) / E) (6b)
Bulk Modulus Fluid Elasticity some common Fluids - E
- water : 2.15 109 (N/m2)
- ethyl alcohol : 1.06 109 (N/m2)
- oil : 1.5 109 (N/m2)
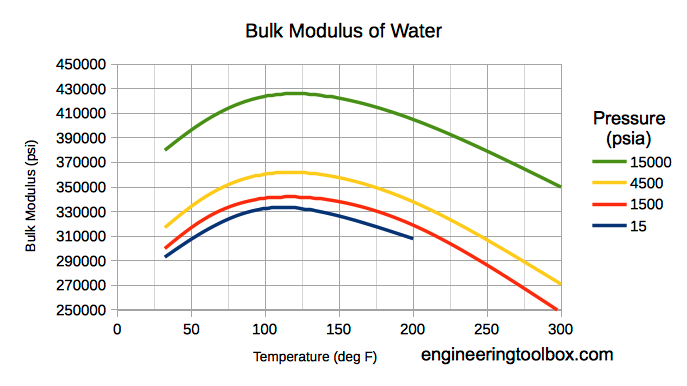
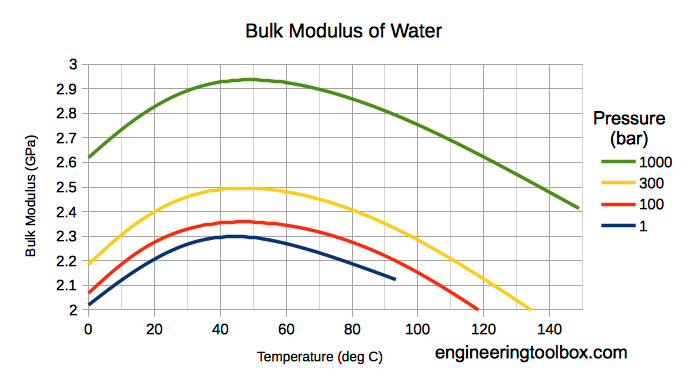
Note! Bulk modulus for liquids varies with pressure and temperature.
Bulk modulus for water - Imperial Units
Bulk modulus for Water - SI units
Density of a fluid changing both Temperature and Pressure
The density of a fluid when changing both temperature and pressure can be expressed combining (4b) and (6b) :
ρ1 = ρ 1(from eq.1) / (1 - (p1 - p0 ) / E)
= ρ0 / (1 + β (t1 - t0 )) / (1 - (p1 - p0 ) / E) (7)
Example - Density of Water at 100 bar and 20 oC
- density of water 0 oC : 999.8 (kg/m3 )
- expansion coefficient of water at 10 oC : 0.000088 ( m3 /m3 oC) (average value between 0 and 20 oC)
- bulk modulus of water: 2.15 109 (N/m2)
Density of water can be calculated with (3):
ρ1 = (999.8 kg/m3 ) / (1 + (0.000088 m3 /m3 oC) ((20 oC) - (0 oC) )) / (1 - ((100 105 Pa) - (1 105 Pa)) / ( 2.15 109 N/m2) )
= 1002.7 (kg/m3 )
Related Topics
-
Densities
Densities of solids, liquids and gases. Definitions and convertion calculators. -
Fluid Mechanics
The study of fluids - liquids and gases. Involving velocity, pressure, density and temperature as functions of space and time. -
Thermodynamics
Work, heat and energy systems.
Related Documents
-
Alcohols and Carboxylic Acids - Physical Data
Molweight, melting and boiling point, density, pKa-values, as well as number of carbon and hydrogen atoms in molecules are given for 150 different alcohols and acids. -
Bulk Modulus and Fluid Elasticities
Introduction to - and definition of - Bulk Modulus Elasticity commonly used to characterize the compressibility of fluids. -
Crude Oil - Density vs. Temperature
Variations in crude oil density are shown as function of temperatur, together with volume correction factors. -
Densities of Aqueous Solutions of Inorganic Chlorides
Changes in density of aqueous solutions with changes in concentration at 20°C. Density of inorganic chlorides in water is plotted as function of wt%, mol/kg water and mol/l solution. -
Densities of Aqueous Solutions of Inorganic Potassium Salts
Changes in density of aqueous solutions with changes in concentration at 20°C. Density of potassium salts in water is plotted as function of wt%, mol/kg water and mol/l solution. -
Densities of Aqueous Solutions of Inorganic Sodium Salts
Changes in density of aqueous solutions with changes in concentration at 20°C. Density of inorganic sodium salts in water is plotted as function of wt%, mol/kg water and mol/l solution. -
Densities of Aqueous Solutions of Organic Acids
Changes in density of aqueous solutions with changes in concentration at 20°C. Density of acetic acid, citric acid, formic acid, D-lactic acid, oxalic acid and trichloroacetic acid in water is plotted as function of wt%, mol/kg water and mol/l solution. -
Densities of common Products
Densities of common products - Imperial and SI-units. -
Density Converter
Online density converter with commonly used units. -
Density of Aqueous Solutions of Organic Substances as Sugars and Alcohols
Changes in density of aqueous solutions with changes in concentration at 20°C. Density of some sugars, alcohols and other organic substances in water is plotted as function of wt%, mol/kg water and mol/l solution. -
Density of Aqueous Solutions of some Inorganic Substances
Changes in density of aqueous solutions with changes in concentration at 20°C. Density of inorganic substances in water is plotted as function of wt%, mol/kg water and mol/l solution. -
Density vs. Specific Weight and Specific Gravity
An introduction to density, specific weight and specific gravity. -
Fuel Oils - Densities vs. Temperature
Variations in fuel oils density as function of temperatur, together with volume correction factors. -
Hydrocarbons - Physical Data
Molweight, melting and boiling point, density, flash point and autoignition temperature, as well as number of carbon and hydrogen atoms in each molecule for 200 different hydrocarbons. -
Hydrocarbons, Linear Alcohols and Acids - Densities
Density of hydrocarbons like alcohols and acids as function of carbon number at 20°C / 68°. -
Ice and Water - Melting Points vs. Pressure
Online calculator, figures and tables with melting points of ice to water at pressures ranging from 0 to 29000 psia (0 to 2000 bara). Temperature given as °C, °F, K and °R. -
Jet Fuel - Density vs. Temperature
Variations in jet fuel density as function of temperatur, together with volume correction factors. -
Liquids - Densities
Densities of common liquids like acetone, beer, oil, water and more. -
Liquids - Volumetric Expansion Coefficients
Volumetric - or cubical - expansion coefficients for common liquids. -
Lubricating Oil - Densities vs. Temperature
Variations in lubricating oil density as function of temperatur, together with volume correction factors. -
Minerals - Densities
Densities of minerals. -
Organic Sulfur Compounds - Densities
Liquid density of different kinds of organic sulfur compounds with varying carbon number (20°C/68°F). Comparison of thiols, sulfides, disulfides and thiophenes. -
Volumetric (Cubic) Thermal Expansion
Volumetric temperature expansion calculator. -
Water - Density, Specific Weight and Thermal Expansion Coefficients
Definitions, online calculator and figures and tables with water properties like density, specific weight and thermal expansion coefficient of liquid water at temperatures ranging 0 to 360°C (32 to 680°F). -
Water - Saturation Pressure vs. Temperature
Online calculator, figures and tables with water saturation (vapor) pressure at temperatures ranging 0 to 370 °C (32 to 700°F) - in Imperial and SI Units. -
Water - Thermophysical Properties
Thermal properties of water at different temperatures like density, freezing temperature, boiling temperature, latent heat of melting, latent heat of evaporation, critical temperature and more.




