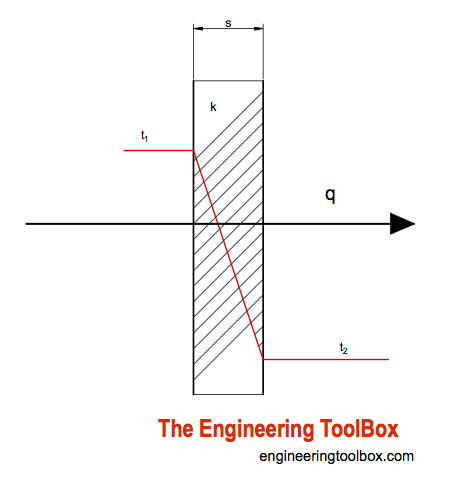
Conductive Heat Transfer
Conductive heat transfer takes place in a solid if there is a temperature gradient.
Conduction as heat transfer takes place if there is a temperature gradient in a solid or stationary fluid medium.
With conduction energy transfers from more energetic to less energetic molecules when neighboring molecules collide. Heat flows in direction of decreasing temperatures since higher temperatures are associated with higher molecular energy.
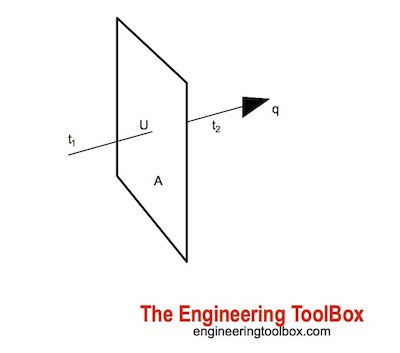
Conductive heat transfer can be expressed with "Fourier's Law"
q = (k / s) A dT
= U A dT (1)
where
q = heat transfer (W, J/s, Btu/hr)
k = Thermal Conductivity of material (W/m K or W/moC, Btu/(hr oF ft2/ft))
s = material thickness (m, ft)
A = heat transfer area (m2, ft2)
U = k / s
= Coefficient of Heat Transfer (W/(m2K), Btu/(ft2 h oF)
dT = t1 - t2
= temperature gradient - difference - over the material (oC, oF)
Example - Conductive Heat Transfer
A plane wall is constructed of solid iron with thermal conductivity 70 W/moC. Thickness of the wall is 50 mm and surface length and width is 1 m by 1 m. The temperature is 150 oC on one side of the surface and 80 oC on the other.
The conductive heat transfer through the wall can be calculated
q = ((70 W/moC) / (0.05 m)) ((1 m) (1 m)) ((150 oC) - (80 oC))
= 98000 (W)
= 98 (kW)
Conductive Heat Transfer Calculator.
This calculator can be used to calculate conductive heat transfer through a wall. The calculator is generic and can be used for both metric and imperial units as long as the use of units is consistent.
Conductive Heat Transfer through a Plane Surface or Wall with Layers in Series

The heat conducted through a wall with layers in thermal contact can be calculated as
q = dT A / ((s1 / k1) + (s2 / k2) + ... + (sn / kn)) (2)
where
dT = t1 - t2
= temperature difference between inside and outside wall (oC, oF)
Note that heat resistance due to surface convection and radiation is not included in this equation. Convection and radiation in general have major impact on the overall heat transfer coefficients.
Example - Conductive Heat Transfer through a Furnace Wall
A furnace wall of 1 m2 consist of 1.2 cm thick stainless steel inner layer covered with 5 cm outside insulation layer of insulation board. The inside surface temperature of the steel is 800 K and the outside surface temperature of the insulation board is 350 K. The thermal conductivity of the stainless steel is 19 W/(m K) and the thermal conductivity of the insulation board is 0.7 W/(m K).
The conductive heat transport through the layered wall can be calculated as
q = ((800 K) - (350 K)) (1 m2) / (((0.012 m) / (19 W/(m K))) + ((0.05 m) / (0.7 W/(m K))))
= 6245 (W)
= 6.25 kW
Thermal Conductivity Units
- Btu/(h ft2 oF/ft)
- Btu/(h ft2 oF/in)
- Btu/(s ft2 oF/ft)
- Btu in)/(ft² h °F)
- MW/(m2 K/m)
- kW/(m2 K/m)
- W/(m2 K/m)
- W/(m2 K/cm)
- W/(cm2 oC/cm)
- W/(in2 oF/in)
- kJ/(h m2 K/m)
- J/(s m2 oC/m)
- kcal/(h m2 oC/m)
- cal/(s cm2 oC/cm)
- 1 W/(m K) = 1 W/(m oC) = 0.85984 kcal/(h m oC) = 0.5779 Btu/(ft h oF) = 0.048 Btu/(in h oF) = 6.935 (Btu in)/(ft² h °F)