Solids - Volumes and Surfaces

Cube

 

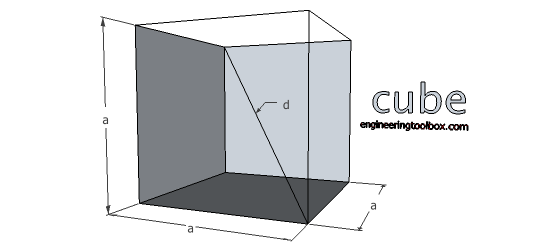
• all figures made with SketchUp and the Engineering ToolBox SketchUp Extension

Volume

V = a³                                (1)

where

V = volume (m³, ft³)

a = side (m, ft)

Surface Area

A₀ = 6 a²                               (1b)

where

A₀ = surface area (m², ft²)

Diagonal

d = a 3^1/2                               (1c)

where

d = inside diagonal (m, ft)

Diagonal of Cube Face

d_s = a 2^1/2                            (1d)

Cuboid - Square Prism

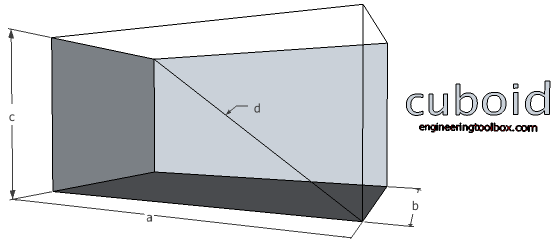
Volume

V = a b c                                    (2)

where

V = volume of solid (m³, ft³)

a = length of rectangular prism (m, ft)

b = width of rectangular prism (m, ft)

c = height of rectangular prism (m, ft)

Diagonal

d =  (a^₂ + b^₂ + c^₂)^1/2                                 (2b)

Surface Area

A₀ = 2 (a b + a c + b c)                                   (2c)

where

A₀ = surface area of solid (m², ft²)

length

width

height

m dm cm mm in ft

Volume:  

Surface:  

Parallelepiped

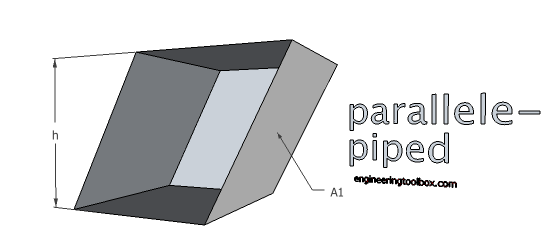
Volume

V = A₁ h                                    (3a)

where

A₁ = side area (m², ft²)

Related Sketchup Components from The Engineering ToolBox

• Geometric Figures - Cylinders, Boxes, Cones, Planes, Spheres, Lines, Curves and more..

- free Engineering ToolBox plugin for use with the amazing Sketchup 3D drawing/model application.

Cylinder

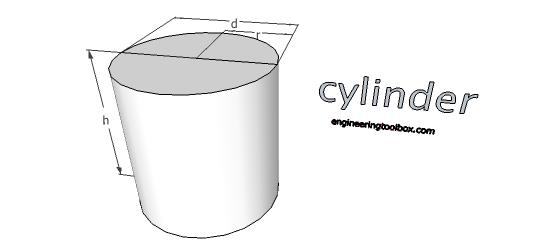
Volume

V = π r² h = (π / 4) d² h                        (4a)

where

d = diameter of cylinder (m, ft)

r = radius of cylinder (m, ft)

h = height of cylinder (m, ft)

Surface

A = 2 π r h + 2 π r²                          (4b)

radius

height

m dm cm mm in ft

Volume:  

Surface:  

Hollow Cylinder

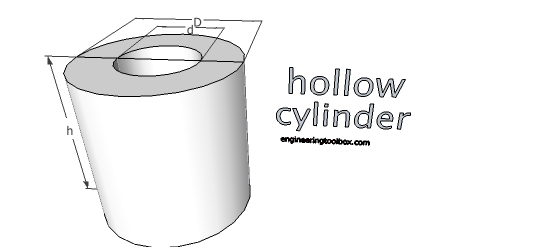
Volume

V = π/4 h (D² - d²)                               (5)

Pyramid

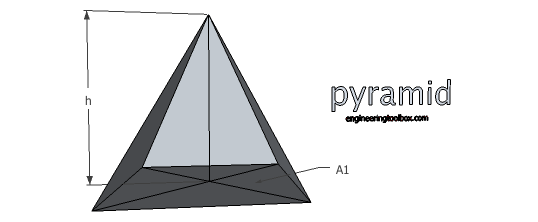
Volume

V = 1/3 h A₁                      (6)

where

A₁ = area of base (m², ft²)

h = perpendicular height of pyramid (m, ft)

Surface

A = ∑ sum of areas of triangles forming sides + A_b                           (6b)

where

the surface areas of the triangular faces will have different formulas for different shaped bases

area of base

perpendicular height

m dm cm mm in ft

Volume:  

Frustum of Pyramid

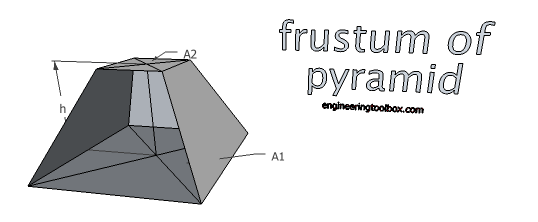
Volume

V = h/3 ( A₁ + A₂ + (A₁ A₂)^1/2)                                     (7)

Cone

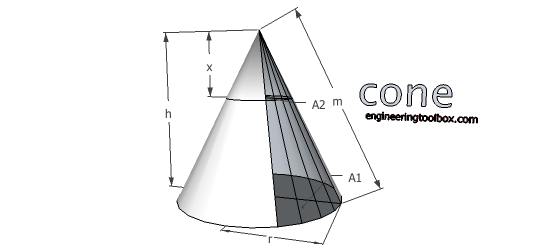
Volume

V = 1/3 π r² h                              (8a)

where

r = radius of cone base (m, ft)

h = height of cone (m, ft)

Surface

A = π r l + π r²                              (8b)

where

l = (r² + h²)^1/2 = length of cone side (m, ft)

radius

height

m dm cm mm in ft

Volume:  

Surface:  

Side

m = (h² + r²)^1/2                             (8c)

 

A₂ / A₁ = x² / h²                             (8d)

Frustum of Cone

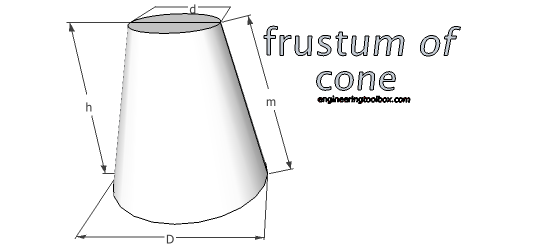
Volume

V = π/12 h (D² + D d + d²)                              (9a)

m = ( ( (D - d) / 2 )² + h²)^1/2                                (9c)

Sphere

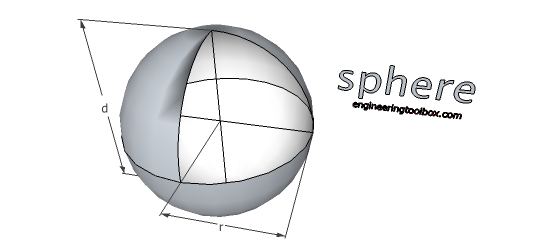
Volume

V = 4/3 π r³  

= 1/6 π d³                                    (10a)

where

r = radius of sphere (m, ft)

Surface

A = 4 π r² 

= π d²     (10b)

radius

m dm cm mm in ft

Volume:  

Surface:  

Spheres with Fractional Diameters - Surface Area and Volume

Fraction Diameter - d – (inch)	Decimal Diameter - d – (inch)	Decimal Radius – r – (inch)	Surface Area - A – (in2)	Volume - V - (in3)
1/64	0.015625	0.007813	0.0007670	0.0000020
1/32	0.031250	0.015625	0.0030680	0.0000160
3/64	0.046875	0.023438	0.0069029	0.0000539
1/64	0.062500	0.031250	0.0122718	0.0001278
5/64	0.078125	0.039063	0.0191748	0.0002497
3/32	0.093750	0.046875	0.0276117	0.0004314
7/64	0.109375	0.054688	0.0375825	0.0006851
1/8	0.125000	0.062500	0.0490874	0.0010227
9/64	0.140625	0.070313	0.0621262	0.0014561
5/32	0.156250	0.078125	0.0766990	0.0019974
11/64	0.171875	0.085938	0.0928058	0.0026585
3/16	0.187500	0.093750	0.1104466	0.0034515
13/64	0.203125	0.101563	0.1296214	0.0043882
7/32	0.218750	0.109375	0.1503301	0.0054808
15/64	0.234375	0.117188	0.1725728	0.0067411
1/4	0.250000	0.125000	0.1963495	0.0081812
17/64	0.265625	0.132813	0.2216602	0.0098131
9/32	0.281250	0.140625	0.2485049	0.0116487
19/64	0.296875	0.148438	0.2768835	0.0137000
5/16	0.312500	0.156250	0.3067962	0.0159790
21/64	0.328125	0.164063	0.3382428	0.0184977
11/32	0.343750	0.171875	0.3712234	0.0212680
23/64	0.359375	0.179688	0.4057379	0.0243020
3/8	0.375000	0.187500	0.4417865	0.0276117
25/64	0.390625	0.195313	0.4793690	0.0312089
13/32	0.406250	0.203125	0.5184855	0.0351058
27/64	0.421875	0.210938	0.5591360	0.0393142
7/16	0.437500	0.218750	0.6013205	0.0438463
29/64	0.453125	0.226563	0.6450389	0.0487139
15/32	0.468750	0.234375	0.6902914	0.0539290
31/64	0.484375	0.242188	0.7370778	0.0595037
1/2	0.500000	0.250000	0.7853982	0.0654498
33/64	0.515625	0.257813	0.8352525	0.0717795
17/32	0.531250	0.265625	0.8866409	0.0785047
35/64	0.546875	0.273438	0.9395632	0.0856373
9/16	0.562500	0.281250	0.9940196	0.0931893
37/64	0.578125	0.289063	1.0500098	0.1011728
19/32	0.593750	0.296875	1.1075341	0.1095997
39/64	0.609375	0.304688	1.1665924	0.1184820
5/8	0.625000	0.312500	1.2271846	0.1278317
41/64	0.640625	0.320313	1.2893109	0.1376608
21/32	0.656250	0.328125	1.3529711	0.1479812
43/64	0.671875	0.335938	1.4181652	0.1588050
11/16	0.687500	0.343750	1.4848934	0.1701440
45/64	0.703125	0.351563	1.5531555	0.1820104
23/32	0.718750	0.359375	1.6229517	0.1944161
47/64	0.734375	0.367188	1.6942818	0.2073730
3/4	0.750000	0.375000	1.7671459	0.2208932
49/64	0.765625	0.382813	1.8415439	0.2349887
25/32	0.781250	0.390625	1.9174760	0.2496714
51/64	0.796875	0.398438	1.9949420	0.2649532
13/16	0.812500	0.406250	2.0739420	0.2808463
53/64	0.828125	0.414063	2.1544760	0.2973626
27/32	0.843750	0.421875	2.2365440	0.3145140
55/64	0.859375	0.429688	2.3201459	0.3323126
7/8	0.875000	0.437500	2.4052819	0.3507703
57/64	0.890625	0.445313	2.4919518	0.3698991
29/32	0.906250	0.453125	2.5801557	0.3897110
59/64	0.921875	0.460938	2.6698936	0.4102180
15/16	0.937500	0.468750	2.7611654	0.4314321
61/64	0.953125	0.476563	2.8539713	0.4533652
31/32	0.968750	0.484375	2.9483111	0.4760294
63/64	0.984375	0.492188	3.0441849	0.4994366
1	1.000000	0.500000	3.1415927	0.5235988

Zone of a Sphere

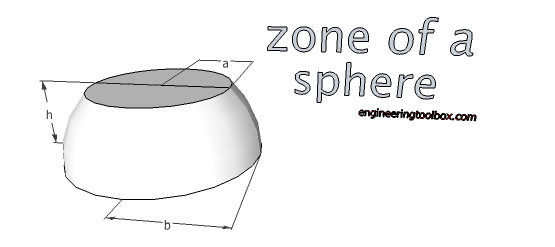
V = π/6 h (3a² + 3b² + h)                             (11a)

A_m = 2 π r h    (11b)

A₀ = π (2 r h + a² + b²)                               (11c)

Segment of a Sphere

V = π/6 h (3/4 s² + h²) 

=   π h² (r - h/3)                                  (12a)

A_m = 2 π r h  

=  π/4 (s² + 4 h²)                               (12b)

Sector of a Sphere

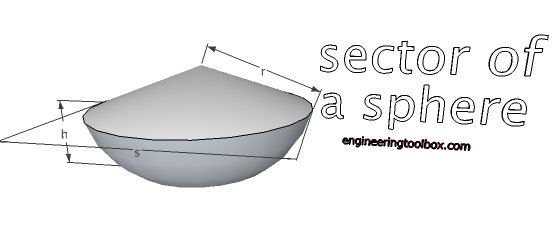
V = 2/3 π r² h                            (13a)

A₀ = π/2 r (4 h + s)                          (13b)

Sphere with Cylindrical Boring

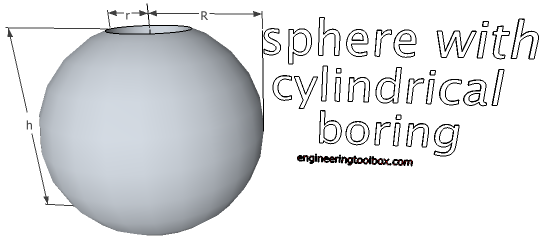
V = π/6  h³                               (14a)

A₀ = 4 π ((R + r)³ (R - r))^1/2  

= 2 π h (R + r)                                (14b)

h = 2 (R² - r²)^1/2                                 (14c)

Sphere with Conical Boring

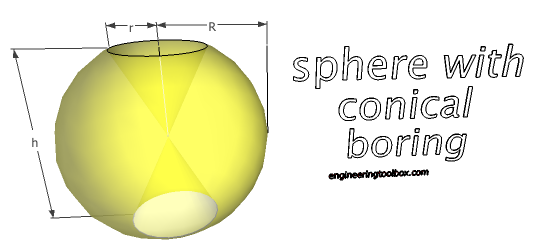
V = 2/3 π R² h                           (15a)

A₀ = 2 π R (h + (R² - h²/4)^1/2)                              (15b)

h = 2 (R² - r²)^1/2                           (15c)

Torus

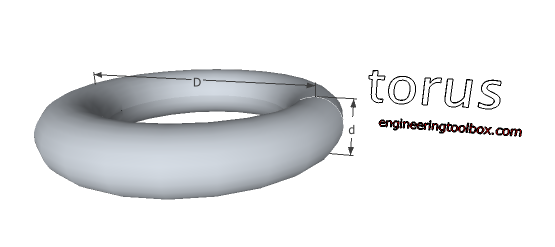
V = π²/4 D d²                           (16a)

A₀ = π² D d                            (16b)

Sliced Cylinder

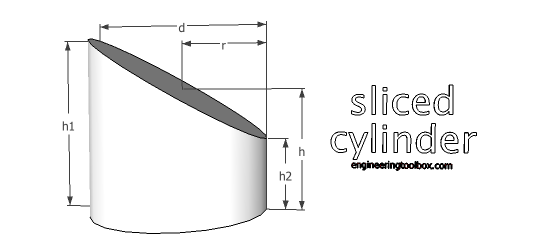
V = π/4 d² h  

   = π r² ((h₁ + h₂) / 2)                           (17a)

A_m = π d h   

     = 2 π r ((h₁ + h₂) / 2)                          (17b)

where

A_m = side walls area

A₀ = π r (h₁ + h₂ + r + (r² + (h₁ - h₂)²/4)^1/2)                                (17c)

where

A₀ = surface area

Ungula

V = 2/3 r² h            (18a)

A_m = 2 r h              (18b)

A₀ = A_m + π/2 r² + π/2 r (r² + h²)^1/2                                      (18c)

Barrel

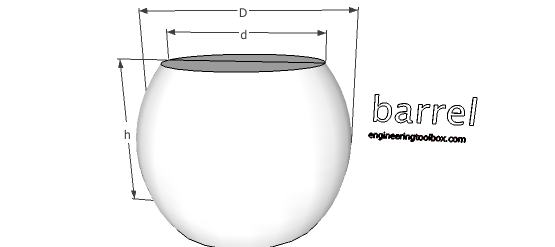
V ≈ π/12 h (2 D² + d²)                                  (19a)

Temperature ^oC
K
^oF

Length m
km
in
ft
yards
miles
naut miles

Area m²
km²
in²
ft²
miles²
acres

Volume m³
liters
in³
ft³
us gal

Weight kg_f
N
lbf

Velocity m/s
km/h
ft/min
ft/s
mph
knots

Pressure Pa
bar
mm H₂O
kg/cm²
psi
inches H₂O

Flow m³/s
m³/h
US gpm
cfm