Interest Rate
Interest rate is the cost of money.
Interest is the cost of money and is measured by the interest rate where
interest rate = cost of having money available for use
The interest rate is a percentage that is periodically added to an amount of money over a specified length of time. If money is borrowed the interest rate is the percentage of the borrowed amount that is paid to the borrower as a compensation for the use of the borrowed property.
Interest reflects that
- money available today has a greater value that money received in the future
The future value of a present amount of value can be expressed as
F = P (1 + i)n (1)
where
F = future value
P = present value
i = interest rate per period
n = number of interest periods
Example - Accumulated Value
The accumulated value of an amount of present value 1 today with interest rate 10% in a 10 years period can be expressed as
| Year | Accumulated Value |
|---|---|
| 0 | 1 |
| 1 | 1.1 |
| 2 | 1.21 |
| 3 | 1.33 |
| 4 | 1.46 |
| 5 | 1.61 |
| 6 | 1.77 |
| 7 | 1.94 |
| 8 | 2.14 |
| 9 | 2.36 |
| 10 | 2.59 |
An amount of 500 will accumulate with the factor 2.14 in 8 years - or
F = 2.14 (500)
= 1070
Future Value of Present Money due to Interest Rate - Calculator Table
This calculated table visualizes the increase in future value of present money due to interest rate and time.
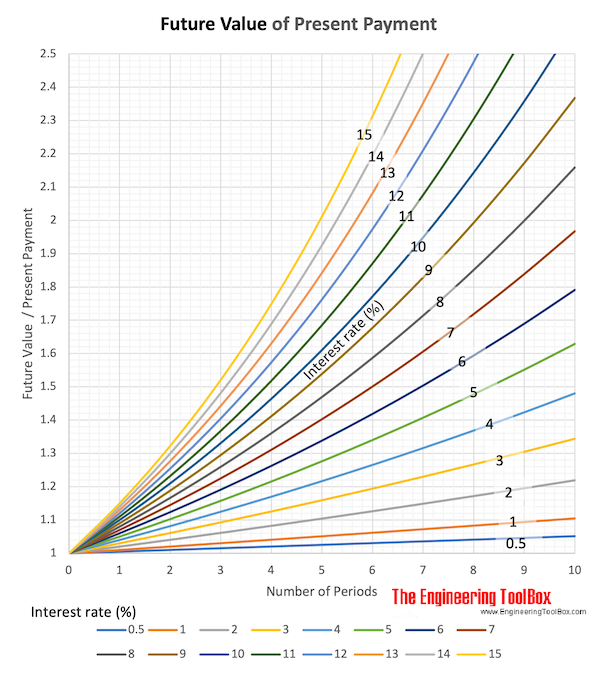
Download and print Future Value of Present Payment chart
Interest Rate - Online Calculator
Finding Unknown Interest Rate
If a single payment P shall produce a future value F after n annual compounding periods, the per annum decimal interest rate can be calculated as
i = (F / P)1/n - 1 (2)
Example - Finding Interest Rate
A single payment of 100 today shall grow to 120 in 5 years. The required interest rate can be calculated as
i = (120 / 100)1/5 - 1
= 0.037
= 3.7 %



