Discrete Compounding Cash Flow Formulas
Discrete payments compounding equations and online calculators .
Single Payment
Compound Amount
Converts a single payment (or value) today - to a future value.
F = P [(1 + i)n] (1)
where
F = future value
P = single payment today
i = interest rate per period
n = number of periods
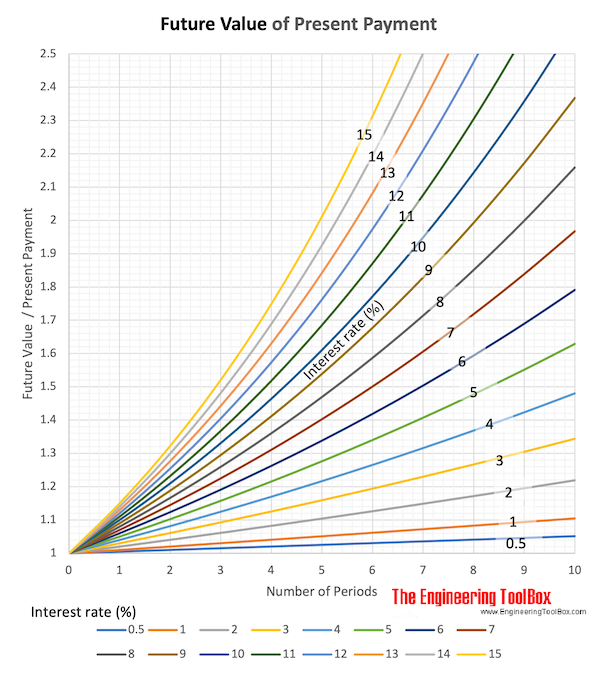
Download and print Future Value of Present Payment chart
Example - Future Value of an Initial Amount Received Today
An amount of 5000 is received today. Calculate the future value of this amount after 7 years with interest rate 5%.
The interest rate can be calculated
i = (5 %) / /100 %)
= 0.05
The future value of the amount can be calculated
F = (5000) [(1 + 0.05)7]
= 7036
Future Value - Online Calculator
Note that interest rate in % is used in the calculator - not in the equation.
Present Worth (or Value)
Converts a future payment (or value) - to present wort (or value).
P = F [(1 + i)-n] (2)
where
P = present value
F = single future payment
i = discount rate per period
n = number of periods
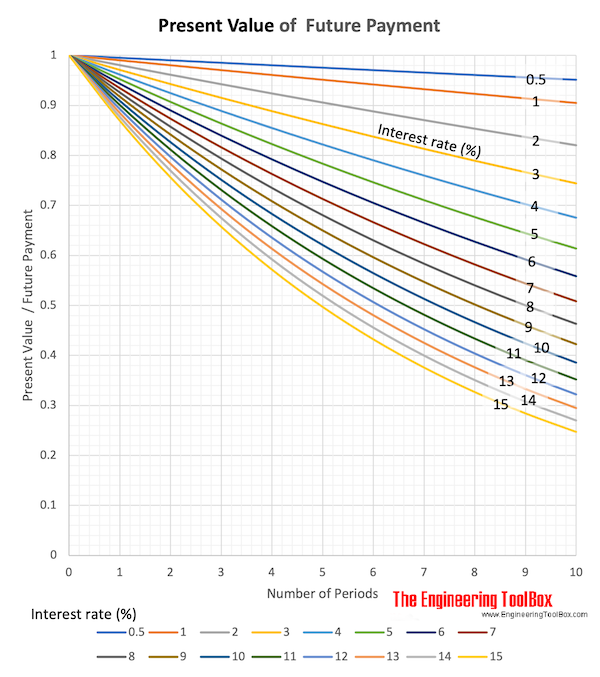
Download and print Present Value of Future Payment chart
Example - Present Value of a Future Payment
An payment of 5000 is received after 7 years. Calculate the present worth (or value) of this payment with dicount rate 5%.
The discount rate can be calculated
i = (5 %) / /100 %)
= 0.05
The present worth of the future payment can be calculated
F = (5000) [(1 + 0.05)-7]
= 3553
Present Value - Online Calculator
Note that discount rate in % is used in the calculator - not in the equation.
Uniform Series
Compound Amount - Annuity
Converts a uniform amount (annuity) - to a future value.
F = A [((1 + i)n - 1) / i ] (3)
where
F = future value
A = uniform amount per period
i = interest rate
n = numbers of periods
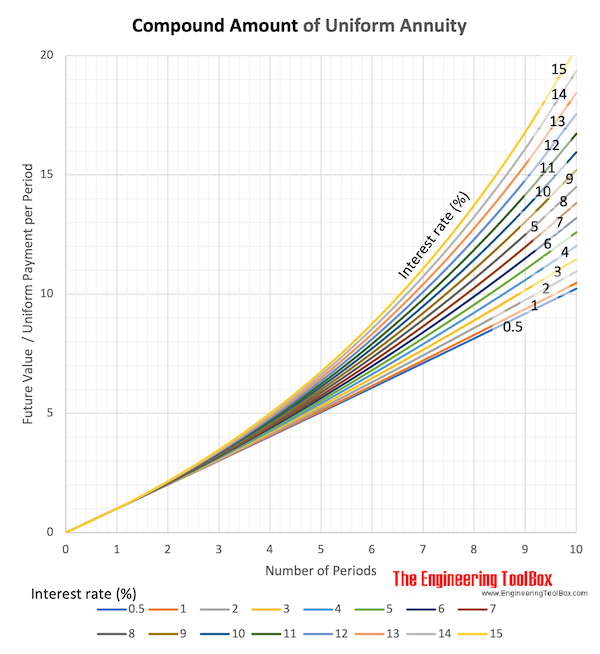Download and print Compound Ammount of Uniform Annuity chart
Example - Present Value of Uniforms Payments
An uniform amount of 5000 is paid every year in 7 years. Calculate the future value of this amount with interest rate 5%.
The interest rate can be calculated
i = (5 %) / /100 %)
= 0.05
The future value of the annuity can be calculated
F = 5000 [((1 + 0.05)7 - 1 ) / 0.05]
= 40710
Compound Amount - Online Calculator
Note that interest rate ín % is used in the calculator - not in the equation.
Sinking Fund
Converts a specific future value to uniform amounts (annuities).
A = F [i / ((1 + i)n - 1)] (4)
where
A = uniform amount per period
F = future value
i = interest rate
n = number of periods
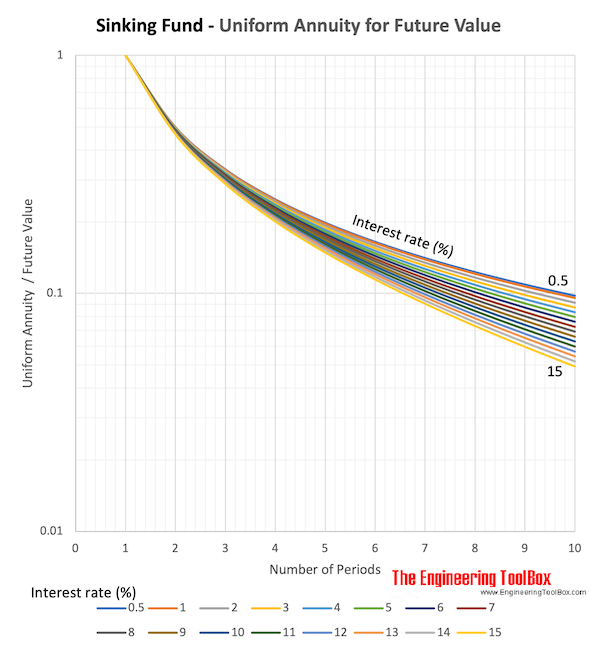
Download and print Sinking Fund - Uniform Annuity to Future Value chart
Example - Uniforms Payments required to reach a Future Value
The future value of a 7 years annuity is 5000. Calculate the required annuity to reach this value with interest rate 5%.
The interest rate can be calculated
i = (5 %) / /100 %)
= 0.05
The uniform payments (annuity) can be calculated
A = 5000 [0.05 / ((1 + 0.05)7 - 1)]
= 614
Sinking Fund - Online Calculator
Note that interest rate in % is used in the calculator - not in the equation.
Present Worth
Converts a uniform amount (annuity) - to a present value.
P = A [((1 + i)n - 1) / ( i (1 + i)n )] (5)
where
P = present value
A = amount per interest period
i = discount rate
n = discount periods
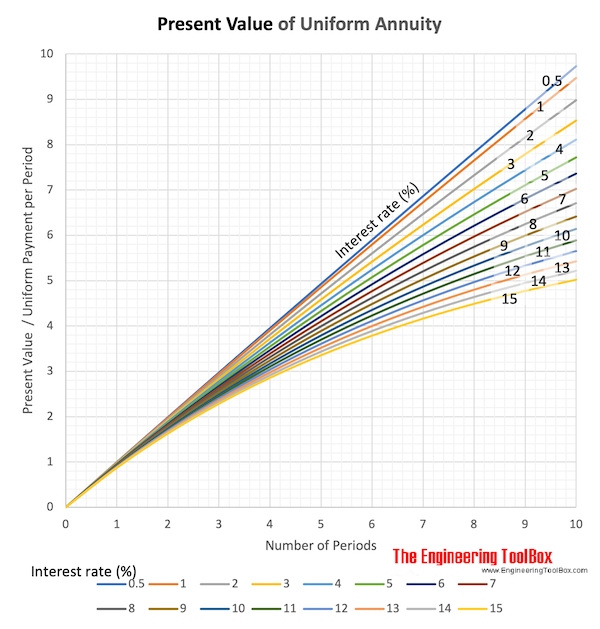
Download and print Present Value of Uniform Annuity chart
Example - Present Value of Uniform Amounts
The uniform amount (annuity) paid from a 7 years project is 5000. Calculate the present value with interest rate 5%.
The interest rate can be calculated
i = (5 %) / /100 %)
= 0.05
The present value of the uniform amounts can be calculated
P = 5000 [((1 + 0.05)7 - 1) / ( 0.05 (1 + 0.05)7 )]
= 28932
Present Worth or Value - Online Calculator
Note that discount rate % is used in the calculator - not in the equation.
Capital Recovery
Converts a present value - to a uniform amount (annuity).
A = P [(i (1 + i)n) / ((1+i)n - 1)] (6)
where
P = present value
A = amount per interest period
i = interest rate
n = discount periods
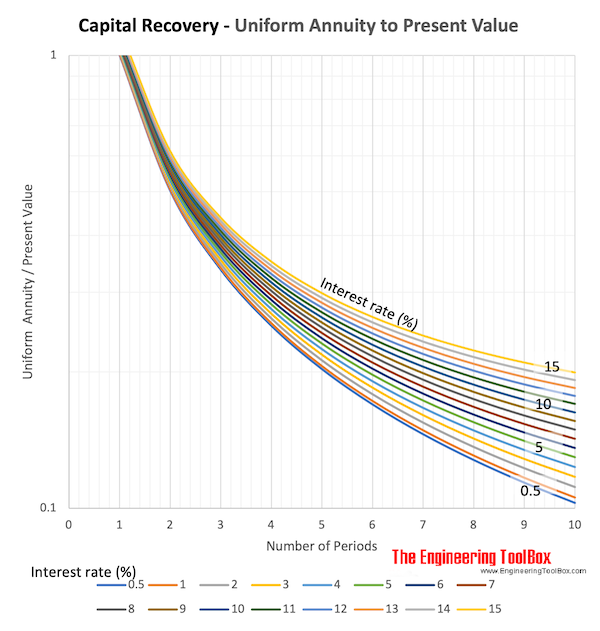Download and print Capital Recovery - Uniform Annuity to Present Value
Capital Recovery - Online Calculator
Note that interest rate in % is used in the calculator - not in the equation.
