Banked Turn
A turn or change of direction in which the vehicle banks or inclines, usually towards the inside of the turn.
For a vehicle moving in a circle - like a train or a car in a curve - the wheels on the vehicle produces a centripetal acceleration toward the center of the circle. The road or track experiences a centrifugal thrust that tries to move the road or track outwards.
The outwards thrust can be reduced by inclining the outside of the track. The inclined angle - or banked angle - is the angle at which a vehicle is inclined about its longitudinal axis with respect to its path.

The banked angle can be calculated in radians as
Θrad = tan-1(v2 / (r ag )) (1)
where
Θrad = banked angle (rad)
v = velocity (m/s)
r = radius of the curve (m)
ag = acceleration of gravity (9.91 m/s2)
- or alternatively in degrees
Θdegrees = tan-1(v2 / (r ag )) (360 / 2 π) (1b)
Example - A Train on a Railway Track in a Curve with Radius 1000 m with Speed 70 km/h
The required banked angle to avoid the centrifugal force can be calculated:
Θ = tan-1(((70 km/h) ( 1000 m/km) / (3600 s/h))2/ ((1000 m) (9.81 m/s2)))
= 0.0385 rad
= (0.0385 rad) (360 / 2 π)
= 2.2o
Banked Turn Calculator
This calculator can be used to calculate the centripetal acceleration of the car and the banked angle.
Road Banked Turn Diagram
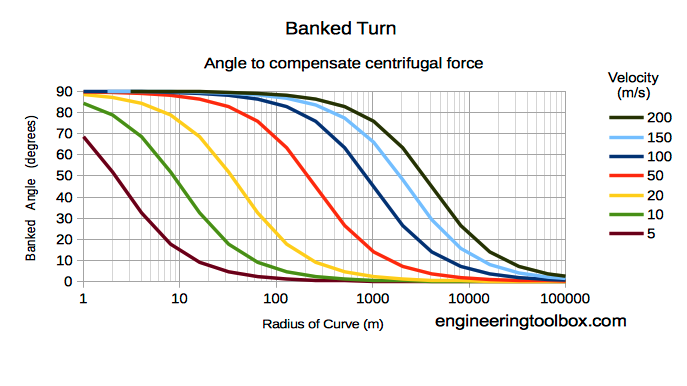
The diagram below indicates velocity vs. curve radius and required banked turn to compensate centrifugal forces.