Mass Moment of Inertia

The Mass Moment of Inertia vs. mass of object, it's shape and relative point of rotation - the Radius of Gyration.

Example - Moment of Inertia of a Single Mass

Moment of inertia

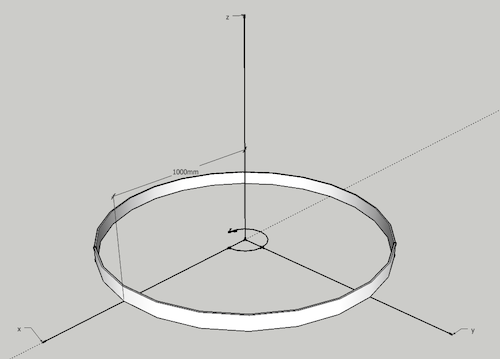
make 3D models with the free Engineering ToolBox Sketchup Extension

The Moment of Inertia with respect to rotation around the z-axis of a single mass of 1 kg distributed as a thin ring as indicated in the figure above, can be calculated as

I_z = (1 kg) ((1000 mm) (0.001 m/mm))²

= 1 kg m²

Moment of Inertia - Distributed Masses

Point mass is the basis for all other moments of inertia since any object can be "built up" from a collection of point masses.

I = ∑_i m_i r_i² = m₁ r₁² + m₂ r₂² + ..... + m_nr_n²(2)

For rigid bodies with continuous distribution of adjacent particles the formula is better expressed as an integral

I = ∫ r² dm (2b)

where

dm = mass of an infinitesimally small part of the body

Convert between Units for the Moment of Inertia

Moment of Inertia Units Converter
Multiply with
from	to
from	kg m²	g cm²	lb_m ft²	lb_m in²	slug ft²	slug in²
kg m²	1	1 10⁷	2.37 10¹	3.42 10³	7.38 10^-1	1.06 10²
g cm²	1 10^-7	1	2.37 10^-6	3.42 10^-4	7.38 10^-8	1.06 10⁵
lb_m ft²	4.21 10^-2	4.21 10⁵	1	1.44 10²	3.11 10^-2	4.48
lb_m in²	2.93 10^-4	2.93 10³	6.94 10^-3	1	2.16 10^-4	3.11 10^-2
slug ft²	1.36	1.36 10⁷	3.22 10¹	4.63 10³	1	1.44 10²
slug in²	9.42 10^-3	9.42 10⁴	2.23 10^-1	3.22 10¹	6.94 10^-3	1

Moment of Inertia - General Formula

A generic expression of the inertia equation is

I = k m r² (2c)

where

k = inertial constant - depending on the shape of the body

Radius of Gyration (in Mechanics)

The Radius of Gyration is the distance from the rotation axis where a concentrated point mass equals the Moment of Inertia of the actual body. The Radius of Gyration for a body can be expressed as

r_g = (I / m)^1/2 (2d)

where

r_g = radius of gyration (m, ft)

I = moment of inertia for the body (kg m², slug ft²)

m = mass of the body (kg, slugs)

vs. Radius of Gyration in Structural Engineering

Some Typical Bodies and their Moments of Inertia

Cylinder

Thin-walled hollow cylinder

Moments of Inertia for a thin-walled hollow cylinder is comparable with the point mass (1) and can be expressed as:

I = m r² (3a)

where

m = mass of the hollow (kg, slugs)

r = distance between axis and the thin walled hollow (m, ft)

r_o = distance between axis and outside hollow (m, ft)

Hollow cylinder

I = 1/2 m (r_i² + r_o²) (3b)

where

m = mass of hollow (kg, slugs)

r_i = distance between axis and inside hollow (m, ft)

r_o = distance between axis and outside hollow (m, ft)

Solid cylinder

I = 1/2 m r² (3c)

where

m = mass of cylinder (kg, slugs)

r = distance between axis and outside cylinder (m, ft)

Circular Disk

I = 1/2 m r² (3d)

where

m = mass of disk (kg, slugs)

r = distance between axis and outside disk (m, ft)

Sphere

Thin-walled hollow sphere

I = 2/3 m r² (4a)

where

m = mass of sphere hollow (kg, slugs)

r = distance between axis and hollow (m, ft)

Solid sphere

I = 2/5 m r² (4b)

where

m = mass of sphere (kg, slugs)

r = radius in sphere (m, ft)

Rectangular Plane

Moments of Inertia for a rectangular plane with axis through center can be expressed as

I = 1/12 m (a² + b²) (5)

where

a, b = short and long sides

Moments of Inertia for a rectangular plane with axis along edge can be expressed as

I = 1/3 m a² (5b)

Slender Rod

Moments of Inertia for a slender rod with axis through center can be expressed as

I = 1/12 m L² (6)

where

L = length of rod

Moments of Inertia for a slender rod with axis through end can be expressed as

I = 1/3 m L² (6b)