Three-Hinged Arches - Continuous and Point Loads
Support reactions and bending moments.
Three-Hinged Arch - Continuous Load
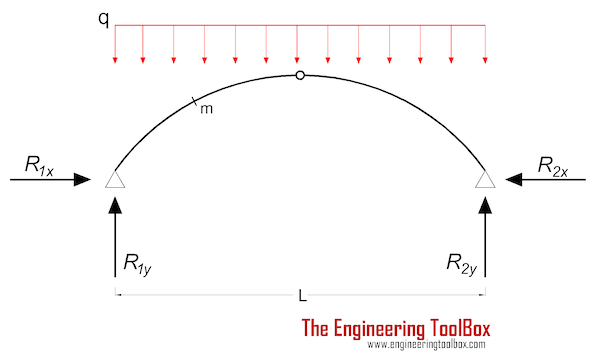Bending Moment
Mm = (q L2 / 8) (4 (xm / L - (xm / L)2) - ym / yc) (1a)
where
Mm = moment at m (Nm, lbf ft)
q = continuous load (N/m, lbf/ft)
xm = x-coordinate for m (m, ft)
ym = y-coordinate for m (m, ft)
yc = y-coordinate for center hinge (m, ft)
L = horizontal distance between the supports (m, ft)
Cartesian coordinates related to a center located in the hinge of support no. 1.
Support Reactions
R1y = R2y
= q L / 2 (1b)
where
R = support force (N, lbf)
R1x = R2x
= q L2 / (8 yc) (1c)
Three-Hinged Arch - Half Continuous Load
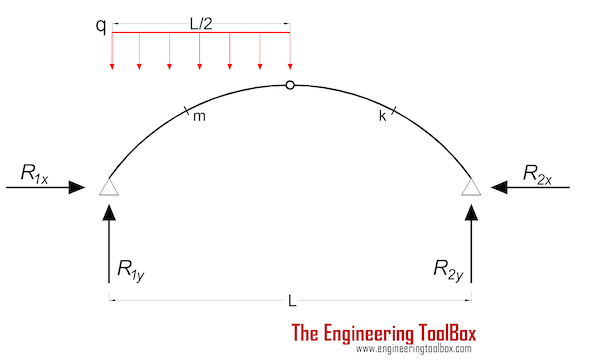Bending Moment
Mm = (q L2 / 16) (8 (xm / L - (xm / L)2) - 2 xm / L - ym / yc) (2a)
Support Reactions
R1y = 3 q L / 8 (2b)
R2y = q L / 8 (2c)
R1x = R2x
= q L2 / (16 yc) (2d)
Three-Hinged Arch - Horizontal Continuous Load
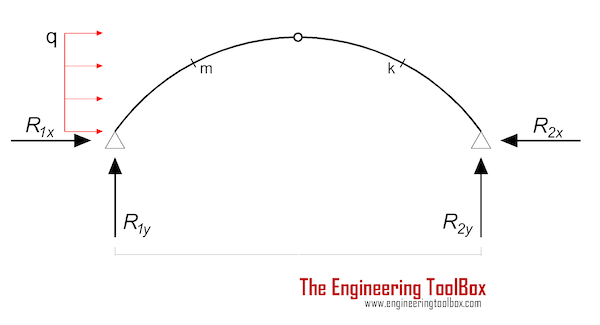Bending Moment
Mm = (q L2 / 2) (xm / L - 3 xm / L + (xm / L)2) (3a)
Mk = (q L2 / 4) (2 (L - xk) / L - yk / yc) (3b)
where
Mk = moment at k (Nm, lbf ft)
yk = y-coordinate for k (m, ft)
xk = x-coordinate for k (m, ft)
Support Reactions
R1y = - q yc2 / (2 L) (3c)
R2y = q yc2 / (2 L) (3d)
R1x = - 3 q yc / 4 (3e)
R2x = q yc / 4 (3f)
Three-Hinged Arch - Eccentric Point Load
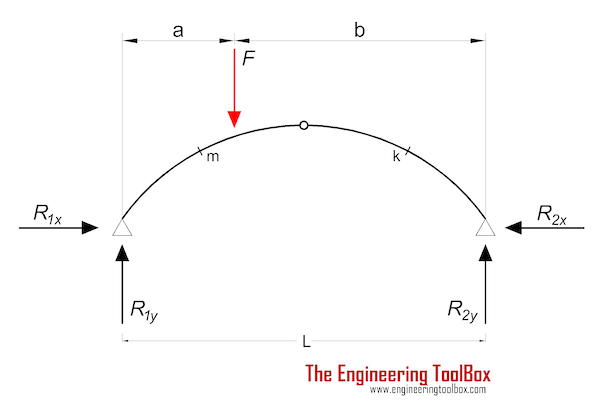Bending Moment
Mm = (F a / 2) (2 (b / a) (xm / L) - ym / yc) (4a)
Mk = (F a /2) (2 (L - xk) / L - yk / yc) (4b)
Support Reactions
R1y = F b / L (4c)
R2y = F a / L (4d)
R1x = R2x
= F a / (2 yc) (4f)
Related Topics
-
Beams and Columns
Deflection and stress in beams and columns, moment of inertia, section modulus and technical information. -
Mechanics
The relationships between forces, acceleration, displacement, vectors, motion, momentum, energy of objects and more. -
Statics
Forces acting on bodies at rest under equilibrium conditions - loads, forces and torque, beams and columns.
Related Documents
-
Area Moment of Inertia - Typical Cross Sections I
Typical cross sections and their Area Moment of Inertia. -
Beams - Fixed at Both Ends - Continuous and Point Loads
Stress, deflections and supporting loads. -
Beams - Fixed at One End and Supported at the Other - Continuous and Point Loads
Supporting loads, moments and deflections. -
Beams - Supported at Both Ends - Continuous and Point Loads
Supporting loads, stress and deflections. -
Cantilever Beams - Moments and Deflections
Maximum reaction forces, deflections and moments - single and uniform loads. -
Continuous Beams - Moment and Reaction Support Forces
Moments and reaction support forces with distributed or point loads. -
Euler's Column Formula
Calculate buckling of columns. -
Mass Moment of Inertia
The Mass Moment of Inertia vs. mass of object, it's shape and relative point of rotation - the Radius of Gyration. -
Stiffness
Stiffness is resistance to deflection. -
Structural Lumber - Properties
Properties of structural lumber. -
Young's Modulus, Tensile Strength and Yield Strength Values for some Materials
Young's Modulus (or Tensile Modulus alt. Modulus of Elasticity) and Ultimate Tensile Strength and Yield Strength for materials like steel, glass, wood and many more.
