Area Moment of Inertia - Typical Cross Sections I
Typical cross sections and their Area Moment of Inertia.
Area Moment of Inertia or Moment of Inertia for an Area - also known as Second Moment of Area - I, is a property of shape that is used to predict deflection, bending and stress in beams.
Area Moment of Inertia - Imperial units
- inches4
Area Moment of Inertia - Metric units
- mm4
- cm4
- m4
Converting between Units
- 1 cm4 = 10-8 m4 = 104 mm4
- 1 in4 = 4.16x105 mm4 = 41.6 cm4
Example - Convert between Area Moment of Inertia Units
9240 cm4 can be converted to mm4 by multiplying with 104
(9240 cm4) 104 = 9.24 107 mm4
Area Moment of Inertia (Moment of Inertia for an Area or Second Moment of Area)
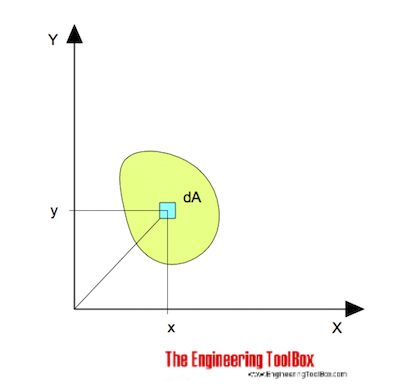
for bending around the x axis can be expressed as
Ix = ∫ y2 dA (1)
where
Ix = Area Moment of Inertia related to the x axis (m4, mm4, inches4)
y = the perpendicular distance from axis x to the element dA (m, mm, inches)
dA = an elemental area (m2, mm2, inches2)
The Moment of Inertia for bending around the y axis can be expressed as
Iy = ∫ x2 dA (2)
where
Iy = Area Moment of Inertia related to the y axis (m4, mm4, inches4)
x = the perpendicular distance from axis y to the element dA (m, mm, inches)
Area Moment of Inertia for typical Cross Sections I
Solid Square Cross Section
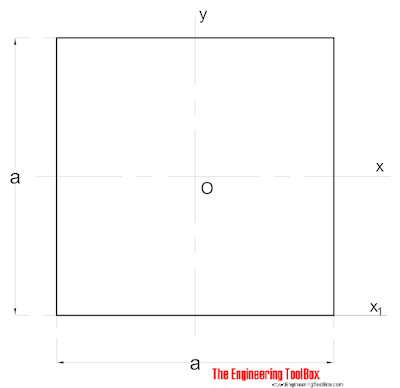
The Area Moment of Inertia for a solid square section can be calculated as
Ix = a4 / 12 (2)
where
a = side (mm, m, in..)
Iy = a4 / 12 (2b)
Solid Rectangular Cross Section
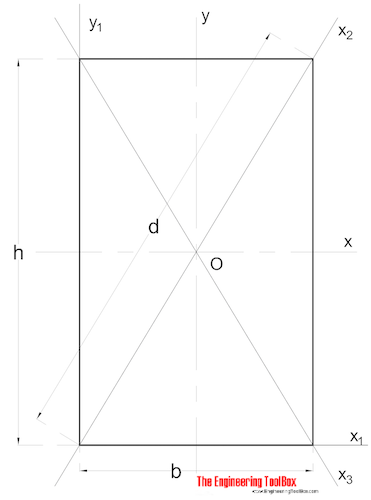
The Area Moment of Ineria for a rectangular section can be calculated as
Ix = b h3 / 12 (3)
where
b = width
h = height
Iy = b3 h / 12 (3b)
Solid Circular Cross Section
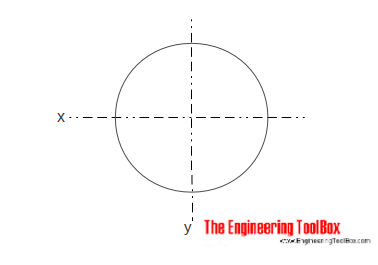
The Area Moment of Inertia for a solid cylindrical section can be calculated as
Ix = π r4 / 4
= π d4 / 64 (4)
where
r = radius
d = diameter
Iy = π r4 / 4
= π d4 / 64 (4b)
Hollow Cylindrical Cross Section
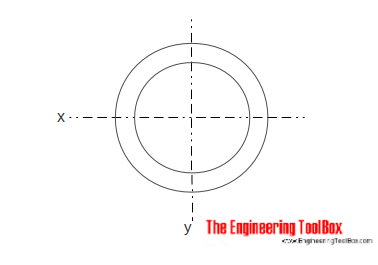
The Area Moment of Inertia for a hollow cylindrical section can be calculated as
Ix = π (do4 - di4) / 64 (5)
where
do = cylinder outside diameter
di = cylinder inside diameter
Iy = π (do4 - di4) / 64 (5b)
Square Section - Diagonal Moments
The diagonal Area Moments of Inertia for a square section can be calculated as
Ix = Iy = a4 / 12 (6)
Rectangular Section - Area Moments on any line through Center of Gravity
Rectangular section and Area of Moment on line through Center of Gravity can be calculated as
Ix = (b h / 12) (h2 cos2 a + b2 sin2 a) (7)
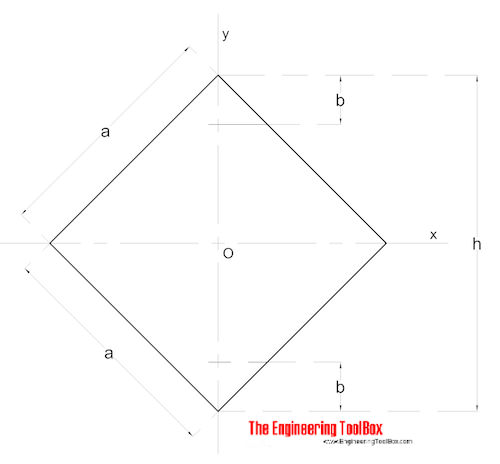
Symmetrical Shape
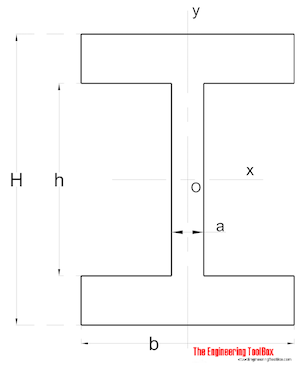
Area Moment of Inertia for a symmetrical shaped section can be calculated as
Ix = (a h3 / 12) + (b / 12) (H3 - h3) (8)
Iy = (a3 h / 12) + (b3 / 12) (H - h) (8b)
Nonsymmetrical Shape
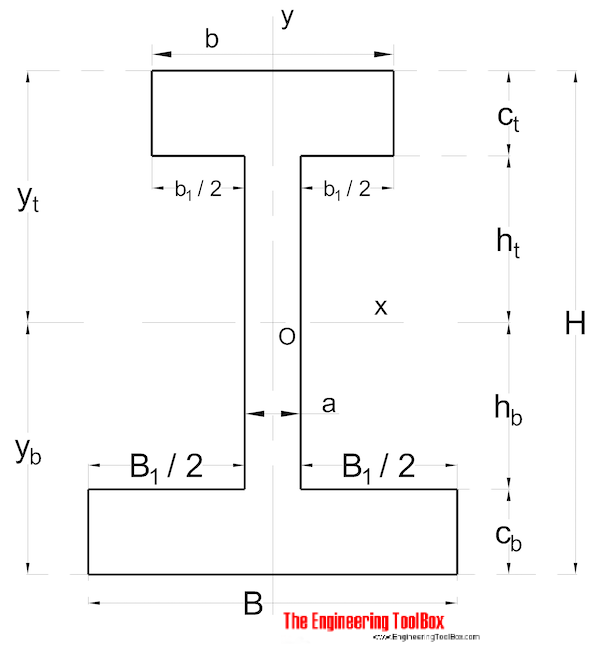
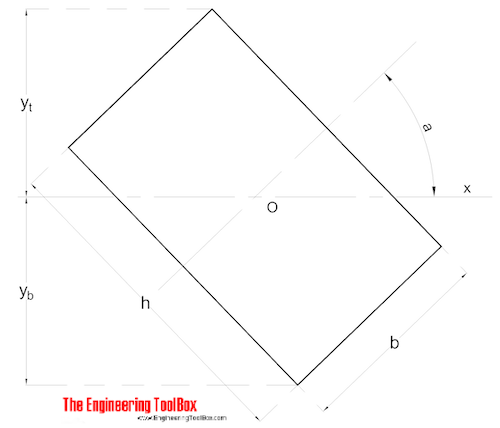
Area Moment of Inertia for a non symmetrical shaped section can be calculated as
Ix = (1 / 3) (B yb3 - B1 hb3 + b yt3 - b1 ht3) (9)
Area Moment of Inertia vs. Polar Moment of Inertia vs. Moment of Inertia
- "Area Moment of Inertia" is a property of shape that is used to predict deflection, bending and stress in beams
- "Polar Moment of Inertia" as a measure of a beam's ability to resist torsion - which is required to calculate the twist of a beam subjected to torque
- "Moment of Inertia" is a measure of an object's resistance to change in rotation direction.
Section Modulus
- the "Section Modulus" is defined as W = I / y, where I is Area Moment of Inertia and y is the distance from the neutral axis to any given fiber
