Euler's Column Formula
Calculate buckling of columns.

Columns fail by buckling when their critical load is reached. Long columns can be analysed with the Euler column formula
F = n π2 E I / L2 (1)
where
F = allowable load (lb, N)
n = factor accounting for the end conditions
E = modulus of elastisity (lb/in2, Pa (N/m2))
L = length of column (in, m)
I = Moment of inertia (in4, m4)
Factor Counting for End Conditions
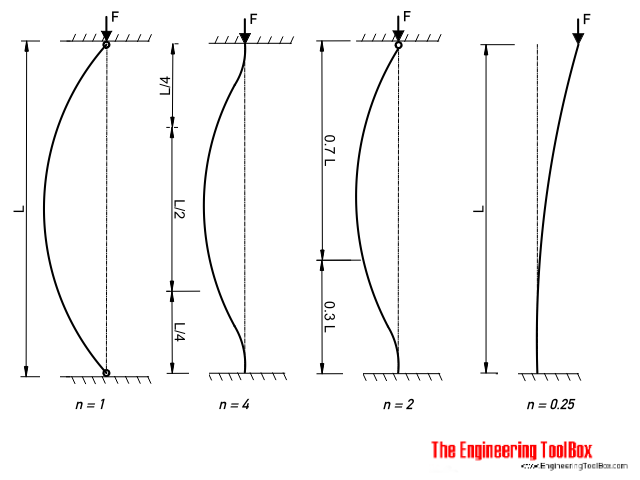
- column pivoted in both ends : n = 1
- both ends fixed : n = 4
- one end fixed, the other end rounded : n = 2
- one end fixed, one end free : n = 0.25
Note!
Equation (1) is sometimes expressed with a k factor accounting for the end conditions:
F = π2 E I / (k L)2 (1b)
where
k = (1 / n)1/2 factor accounting for the end conditions
| n | 1 | 4 | 2 | 0.25 |
| k | 1 | 0.5 | 0.7 | 2 |
Example - A Column Fixed in both Ends
An column with length 5 m is fixed in both ends. The column is made of an Aluminium I-beam 7 x 4 1/2 x 5.80 with a Moment of Inertia iy = 5.78 in4. The Modulus of Elasticity of aluminum is 69 GPa (69 109 Pa) and the factor for a column fixed in both ends is 4.
The Moment of Inertia can be converted to metric units like
Iy = 5.78 in4 (0.0254 m/in)4
= 241 10-8 m4
The Euler buckling load can then be calculated as
F = (4) π2 (69 109 Pa) (241 10-8 m4) / (5 m)2
= 262594 N
= 263 kN
Slenderness Ratio
The term "L/r" is known as the slenderness ratio. L is the length of the column and r is the radiation of gyration for the column.
- higher slenderness ratio - lower critical stress to cause buckling
- lower slenderness ratio - higher critical stress to cause buckling
- slenderness ratios L/r < 40: "short columns" where failure mode is crushing (yielding)
- slenderness ratios 40 < L/r < 120: "intermediate columns" where failure mode is a combination of crushing (yielding) and buckling
- slenderness ratio of 120 < L/r < 200: "long columns" where failure mode is buckling
Related Topics
-
Beams and Columns
Deflection and stress in beams and columns, moment of inertia, section modulus and technical information.
Related Documents
-
Area Moment of Inertia - Typical Cross Sections I
Typical cross sections and their Area Moment of Inertia. -
Area Moment of Inertia - Typical Cross Sections II
Area Moment of Inertia, Moment of Inertia for an Area or Second Moment of Area for typical cross section profiles. -
British Universal Columns and Beams
Properties of British Universal Steel Columns and Beams. -
Concrete Columns
Estimate concrete volume required for concrete columns. -
HE-A Steel Beams
Properties of HE-A profiled steel beams. -
Mass Moment of Inertia
The Mass Moment of Inertia vs. mass of object, it's shape and relative point of rotation - the Radius of Gyration. -
Mild Steel - Square Bars Weight
Typical weights of mild steel square bars. -
Radius of Gyration in Structural Engineering
Radius of gyration describes the distribution of cross sectional area in columns around their centroidal axis. -
Steel Pipe Columns - Allowable Loads
Allowable concentric loads for steel pipe columns. -
Stiffness
Stiffness is resistance to deflection. -
Three-Hinged Arches - Continuous and Point Loads
Support reactions and bending moments. -
W-Beams - American Wide Flange Beams
Dimensions of American Wide Flange Beams ASTM A6 (or W-Beams) - Imperial units. -
Weight of Beams - Stress and Strain
Stress and deformation of vertical beams due to own weight. -
Wood Columns - Safe Loads
Safe loads for wood columns. -
Young's Modulus, Tensile Strength and Yield Strength Values for some Materials
Young's Modulus (or Tensile Modulus alt. Modulus of Elasticity) and Ultimate Tensile Strength and Yield Strength for materials like steel, glass, wood and many more.




