Sound - Attenuation and the Directivity Coefficient
The attenuation in a room depends on the location of the sound source and the receiver - and the room constant.
For a continuing sound source the sound level in a room is the sum of direct and reverberant sound. The sound pressure for a receiver can be expressed as
Lp = LN + log (D / (4 π r2) + 4 / R) (1)
where
Lp = received sound pressure level (dB)
LN = sound power level from source (dB)
D = directivity coefficient
R = room constant (m2 Sabine)
π = 3.14 .....
r = distance from source (m)
Directivity coefficient - D
The figure below can be used to approximate the Directivity coefficient - D - for typical locations of the receiver and the sound source
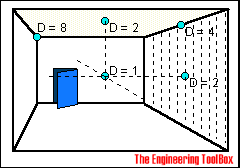
(1) can be transformed to express the difference between the received sound pressure level and emitted sound power level - the attenuation - as:
Lp - LN = 10 log (D / (4 π r2) + 4 / R) (2)
Room Sound Attenuation Calculator
The attenuation (Lp - LN) can also be estimated from the diagram below by modifying (2) to be expressed as the ratio between "distance r between source and receiver" and "square of the directivity coefficient D" - and the total room sound absorption in m2 Sabine.
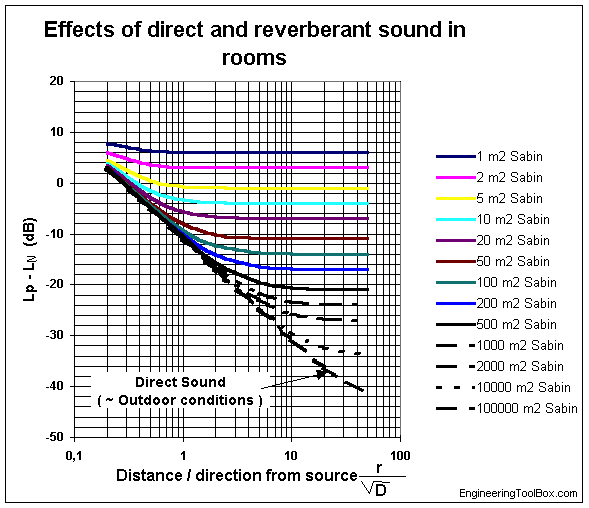
Example - Sound Attenuation in a Room
For a room the acoustic property total room sound absorption is 1000 m2 Sabine. For a listener in the middle of the room with a directivity constant 1 and at distance 1 m from the sound source - the ratio
r / D1/2 = 1 / (1 m)1/2
= 1
From the diagram above the attenuation can estimated to approximately
10 dB
Related Topics
-
Acoustics
Room acoustics and acoustic properties, decibel A, B and C, Noise Rating (NR) curves, sound transmission, sound pressure, sound intensity and sound attenuation. -
Noise and Attenuation
Noise is usually defined as unwanted sound - noise, noise generation, silencers and attenuation in HVAC systems.
Related Documents
-
Benzene - Dynamic and Kinematic Viscosity vs. Temperature and Pressure
Online calculator, figures and table showing dynamic and kinematic viscosity of benzene, C6H6, at varying temperature and pressure - Imperial and SI Units. -
Mercury - Thermodynamic Properties
Properties of saturated liquid Mercury - Hg - density, specific heat capacity, kinematic viscosity, thermal conductivity and Prandtl number. -
Propagation of Sound Indoors - the Room Constant
In a room the sound or noise will reach the receiver as direct and reverberant sound. -
Sound - Abatement vs. the Distance from Source
The disruption of the sound pressure wave and the reduction of noise is called attenuation - Sound Pressure Level vs. distance calculator. -
Sound - Attenuation and Speed vs. Sound Frequency and Air Humidity
The speed and attenuation of sound in moist air varies with sound frequency and air humidity. -
Sound - Room Attenuation in Direct Sound Fields
Room size, absorption characteristics - and attenuation in direct sound fields. -
Sound Attenuation - Duct split to Terminals
Estimating sound attenuation where ducts splits to terminals. -
Sound Attenuation in Duct Elbows
Noise attenuation in duct elbows by reflected sound. -
Sound Power
Sound power from sources like fans, jet engines, cars, humans and more. -
Sound Pressure
Sound Pressure is the force of sound on a surface perpendicular to the propagation of sound.
