Pump - Temperature Rise vs. Volume Flow
Calculate temperature rise vs. volume flow in pumps.
No pump is perfect with 100% efficiency. Energy lost in friction and hydraulic losses transforms to heat - heating up the fluid transported through the pump.
The temperature rise can be calculated as
dt = Ps (1 - μ) / (cp q ρ) (1)
where
dt = temperature rise in the pump (oC)
q = volume flow through pump (m3/s)
Ps = brake power (kW)
cp = specific heat of the fluid (kJ/kgoC)
μ = pump efficiency
ρ = fluid density (kg/m3)
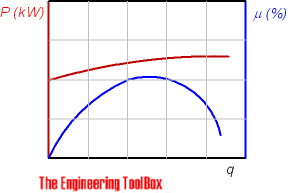
A typical relation between flow, efficiency and power consumption for a centrifugal pump:
Pump - Temperature Rise Calculator
Example - Temperature rise in water pump
Temperature rise in a water pump working at normal conditions with flow 6 m3/h (0.0017 m3/s), brake power 0.11 kW and pump efficiency of 28% (0.28) can be calculated as
dt = (0.11 kW) (1 - 0.28) / ((4.2 kJ/kgoC) (0.0017 m3/s) (1000 kg/m3))
= 0.011 oC
Specific heat of water cp = 4.2 kJ/kgoC.
If the flow through the pump is reduced by throttling the discharge valve the temperature rise increase. If the flow is reduced to 2 m3/h (0.00056 m3/s), brake power slightly reduced to 0.095 kW and the pump efficiency reduced to 15% (0.15) - the temperature rise can be calculated as
dt = (0.095 kW) (1 - 0.15) / ((4.2 kJ/kgoC) (0.00056 m3/s) (1000 kg/m3))
= 0.035 oC
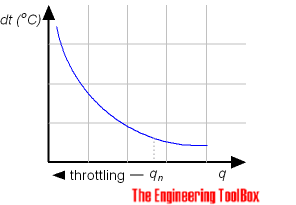
With manufacturing documentation the temperature rise versus throttling can be expressed as:
Related Topics
-
Pumps
Design of pumping systems and pipelines. With centrifugal pumps, displacement pumps, cavitation, fluid viscosity, head and pressure, power consumption and more.
Related Documents
-
BEP - the Best Efficiency Point of a Pump
BEP is where the pump is most efficient. -
Centrifugal Pumps
An introduction to Centrifugal Pumps. -
Centrifugal Pumps - Capacity Modulation
Modulating pumps to adapt capacities to variable process demands. -
Positive Displacement Pumps
Introduction tutorial to positive displacement pumps basic operating principles. -
Pump Power Calculator
Calculate pumps hydraulic and shaft power. -
Pumping Water - Energy Cost Calculator
Calculate the energy cost of pumping water. -
Pumps - Classifications
Centrifugal pumps vs. positive displacement pumps. -
Pumps, Fans and Turbines - Horsepower
British Horse Power as used for pumps, fans and turbines - and how to convert to other units. -
System Curve and Pump Performance Curve
Utilize the system curve and the pump performance curve to select the proper pump for a particular application.




