Pumps, Fans and Turbines - Horsepower

Horsepower

Horsepower is the imperial (British) unit of power. A horsepower is the ability to do work at the rate of

• 33000 ft.lb per min or
• 550 ft.lb per second

Note that Power is "Work per unit time" and work is "Force through distance". In gravity systems the Force is Weight - mass multiplied with gravity.

In the SI system the unit of power is watt (W, Nm/s, J/s).

The total horsepower developed by water falling from a given height is the product of the mass flow rate in pounds per minute times the falling height in feet divided by 33000 and can be expressed as:

P_hp = m_min h a_g / 33000                                 (1)

where

P_hp = power (horsepower, hp)

m_min = mass flow rate per minute (lb_m/min)

h = head or height (ft)

a_g = acceleration of gravity (32 ft/s²)

(1) can alternatively be expressed as:

P_hp = m_sec h a_g / 550                                (1b)

where

m_sec = mass flow rate per second (lb_m/s)

(1) can also be expressed as:

P_hp = γ Q h / 33000                                 (1c)

where

Q = volume flow rate (ft³/min)

γ= specific weight (lb_f/ft³) (weight is force)

Water Horsepower for Flow in gal/min

Water horsepower for flow in gal/min can be expressed as:

P_whp = SG Q_gal h / 3960         (1d)

where

Q = volume flow rate (gpm)

SG= specific gravity

h = head (ft)

SG for water is 1.001 at 32^oF and 0.948 at 240^oF.

• Specific Gravity for some common Fluids and Liquids

SG - Specific Gravity

Q_gal - Volume Flow (imp gpm)

h - head (ft)

Power to Pump Water

Required horsepower (hp) to pump 1 cubic foot of water per minute (ft³/min) with efficiency 85% - is indicated in the diagram below:

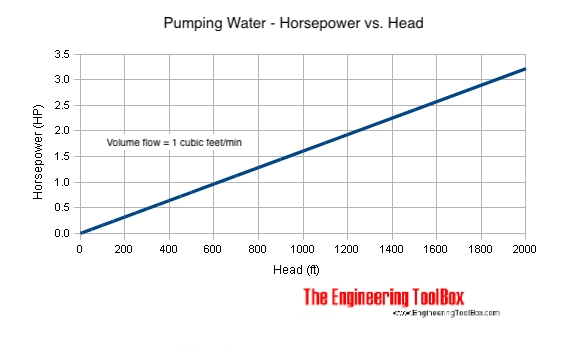
• 1 hp (English horse power) = 745.7 W
• 1 ft (foot) = 0.3048 m

Example - Required Power to lift 10 ft³/min of Water 600 ft

According the diagram above 1 hp is required to lift 1 ft³/min of water 600 ft. Required power to pump 10 ft³/min can be calculated as

(10 ft³/min) (1 hp) / (1 ft³/min) = 10 hp

Shaft or Brake Horsepower

The brake horsepower is the amount of real horsepower going to the pump, not the horsepower used by the motor. In the metric system kilowatts (kW) is used.

Due to hydraulic, mechanical and volumetric losses in a pump or turbine the actual horsepower available for work on or from the fluid is less than the total horsepower supplied.

Shaft or Brake Horsepower for a Pump or Fan

The brake horse power - bhp - for a pump or fan can be expressed as:

P_bhp = ( γ Q h / 33000 ) / η                               (2)

where

P_bhp = brake horse power (horsepower, hp)

Q = volume flow rate (ft³/min, cfm)

η = overall efficiency

Shaft or Brake Horsepower for a Turbine

The brake horse power - bhp - for a turbine can be expressed as:

P_bhp = η ( γ Q h / 33000 )                              (2b)

Input Horsepower to the Electrical Motor

The input horsepower to the electrical motor for a pump or fan can be expressed as:

P_{hp_el} = P_bhp /η_e         (3)

or

P_{hp_el} = (m h g / 33000) / (ηη_e)         (3b)

where

P_{hp_el} = input power to the electrical motor

η_e = mechanical efficiency of the electrical motor

Horsepower in Kilowatts and other Units

Horsepower can be converted to other common units as:

• 1 hp (English horse power) = 745.7 W = 0.746 kW = 550 ft.lb/s = 2545 Btu/h = 33000 ft.lb/m = 1.0139 metric horse power

Transforming horsepower to kW:

P_kW = 0.746 P_hp                             (4)

where

P_kW = power (kW)

Together with the equations above it's possible to express (4) in many common combinations - such as:

P_kW = 0.746 (m h / 33000) / η η_e                             (5)

Example - Pump Power

The horsepower required to pump 50 lb_m/min water a head of 10 ft with a pump with overall efficiency 0.7 - can be calculated with eq. (3) as

P_hp = ((50 lb_m/min)(10 ft) (32 ft/s²) / 33000) / 0.8

       = 0.6 hp

The power in kW can be calculated as 

P_kW = 0.746 (0.6 hp)

       = 0.45 kW

Temperature ^oC
K
^oF

Length m
km
in
ft
yards
miles
naut miles

Area m²
km²
in²
ft²
miles²
acres

Volume m³
liters
in³
ft³
us gal

Weight kg_f
N
lbf

Velocity m/s
km/h
ft/min
ft/s
mph
knots

Pressure Pa
bar
mm H₂O
kg/cm²
psi
inches H₂O

Flow m³/s
m³/h
US gpm
cfm