Kinetic Energy
Energy possessed by an object's motion is kinetic energy.
Work must be done to set any object in motion, and any moving object can do work. Energy is the ability to do work and kinetic energy is the energy of motion. There are several forms of kinetic energy
- vibration - the energy due to vibration motion
- rotational - the energy due to rotational motion
- translational - the energy due to motion from one location to another
Energy has the same units as work and work is force times distance. One Joule is one Newton of force acting through one meter - Nm or Joule in SI-units. The Imperial units are foot-pound.
- 1 ft lb = 1.356 N m (Joule)
Translational Kinetic Energy
Translational kinetic energy can be expressed as
Et = 1/2 m v2 (1)
where
Et = kinetic translation energy (Joule, ft lb)
m = mass (kg, slugs)
v = velocity (m/s, ft/s)
- one slug = 32.1740 pounds (as mass) - lbm
Rotational Kinetic Energy
Rotational kinetic energy can be expressed as
Er = 1/2 I ω2 (2)
where
Em = kinetic rotation energy (Joule, ft lb)
I = moment of inertia - an object's resistance to changes in rotation direction (kg m2, slug ft2)
ω = angular velocity (rad/s)
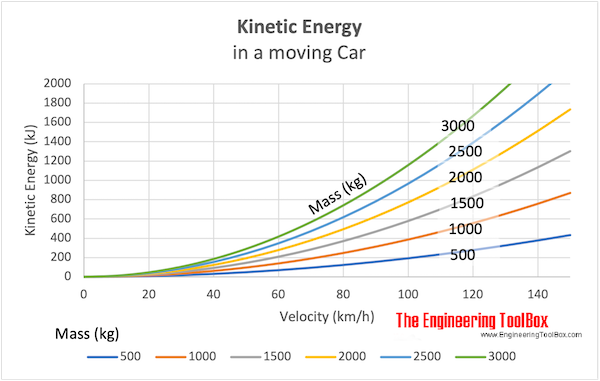
Example - Kinetic Energy in a Car
The kinetic energy of a car with mass of 1000 kg at speed 70 km/h can be calculated as
Et = 1/2 (1000 kg) ((70 km/h) (1000 m/km) / (3600 s/h))2
= 189043 Joule
The kinetic energy of the same car at speed 90 km/h can be expressed as
Et = 1/2 (1000 kg) ((90 km/h) (1000 m/km) / (3600 s/h))2
= 312500 Joule
Note! - when the speed of a car is increased with 28% (from 70 to 90 km/h) - the kinetic energy of the car is increased with 65% (from 189043 to 312500 J). This huge rise in kinetic energy must be absorbed by the safety construction of the car to provide the same protection in a crash - which is very hard to achieve. In a modern car it is possible to survive a crash at 70 km/h. A crash at 90 km/h is more likely fatal.
Download and print Kinetic Energy in a Moving Car chart
Example - Kinetic Energy in a Steel Cube moving on a Conveyor Belt
A steel cube with weight 500 lb is moved on a conveyor belt with a speed of 9 ft/s. The steel cube mass can be calculated as
m = (500 lb) / (32.1740 ft/s2)
= 15.54 slugs
The kinetic energy of the steel cube can be calculated as
Et = 1/2 (15.54 slugs) (9 ft/s)2
= 629 ft lbs
Example - Kinetic Energy in a Flywheel
A flywheel with Moment of Inertia I = 0.15 kg m2 is rotating with 1000 rpm (revolutions/min). The angular velocity can be calculated as
ω = (1000 revolutions/min) (0.01667 min/s) (2 π rad/revolution)
= 104 rad/s
The flywheel kinetic energy can be calculated
Er = 1/2 (0.15 kg m2) (104 rad/s)2
= 821 J
