Formulas of Motion - Linear and Circular
Linear and angular (rotation) acceleration, velocity, speed and distance.
Linear Motion Formulas
Average velocity/speed of a moving object can be calculated as
v = s / t (1a)
where
v = velocity or speed (m/s, ft/s)
s = linear distance traveled (m, ft)
t = time (s)
- distance is the length of the path a body follows in moving from one point to another - displacement is the straight line distance between the initial and final positions of the body
- we use velocity and speed interchangeable - but be aware that speed is a measure of how fast or slow a distance is covered, the rate at which distance is covered - velocity is a vector, specifying how fast or slow a distance is covered and the direction
If acceleration is constant then velocity can be expressed as:
v = v0 + a t (1b)
where
v0 = initial linear velocity (m/s, ft/s)
a = acceleration (m/s2, ft/s2)
Linear distance can be expressed as (if acceleration is constant):
s = v0 t + 1/2 a t2 (1c)
Combining 1b and 1c to express the final velocity
v = (v02+ 2 a s)1/2 (1d)
Velocity can be expressed as (velocity is variable)
v = ds / dt (1f)
where
ds = change in distance (m, ft)
dt = change in time (s)
Acceleration can be expressed as
a = dv / dt (1g)
where
dv = change in velocity (m/s, ft/s)
Example - a Marathon Run
If a marathon - 42195 m - is run in amazing 2:03:23 (7403 seconds) (Wilson Kipsang, Kenya - September 29, 2013 Berlin Marathon) - the average speed can be calculated
v = (42195 m) / (7403 s)
= 5.7 m/s
= 20.5 km/h
Example - Acceleration of a Car
A car accelerates from 0 km/h to 100 km/h in 10 seconds . The acceleration can be calculated by transforming (1b) to
a = (v - v0) / t
= ( (100 km/h) (1000 m/km) / (3600 s/h) - (0 km/h) ( 1000 m/km) / (3600 s/h)) / (10 s)
= 2.78 m/s2
Linear Motion Calculators
Average velocity
Distance
Final Velocity
Acceleration
Circular Motion - Rotation
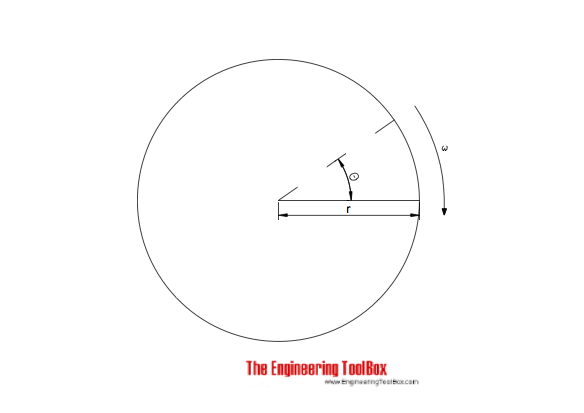
Angular Velocity
Angular velocity can be expressed as (angular velocity = constant):
ω = θ / t (2)
where
ω = angular velocity ( rad/s)
θ = angular distance ( rad)
t = time (s)
Angular velocity and rpm:
ω = 2 π n / 60 (2a)
where
n = revolutions per minute (rpm)
π = 3.14...
The tangential velocity of a point in angular velocity - in metric or imperial units like m/s or ft/s - can be calculated as
v = ω r (2b)
where
v = tangential velocity (m/s, ft/s, in/s)
r = distance from center to the point (m, ft, in)
Example - Tangential Velocity of a Bicycle Tire
A 26 inches bicycle wheel rotates with an angular velocity of π radians/s (0.5 turn per second) . The tangential velocity of the tire can be calculated as
v = ( π radians/s) ((26 inches) / 2)
= 40.8 inches/s
Angular Velocity and Acceleration
Angular velocity can also be expressed as (angular acceleration = constant):
ω = ωo + α t (2c)
where
ωo = angular velocity at time zero ( rad/s)
α = angular acceleration or deceleration (rad/s2)
Angular Displacement
Angular distance can be expressed as (angular acceleration is constant):
θ = ωo t + 1/2 α t2 (2d)
Combining 2a and 2c:
ω = (ωo 2+ 2 α θ)1/2
Angular Acceleration
Angular acceleration can be expressed as:
α = dω / dt
= d2θ / dt2 (2e)
where
dθ = change of angular distance (rad)
dt = change in time (s)
Example - Flywheel Deceleration
By Geni (Photo by User:geni) ( GFDL or CC-BY-SA-3.0-2.5-2.0-1.0 ), via Wikimedia Commons
A flywheel is slowed down from 2000 rpm ( revolutions /min) to 1800 rpm in 10 s . The deceleration of the flywheel can be calculated as
α = ((2000 rev/min) - (1800 rev/min)) (0.01667 min/s) (2 π rad/rev) / (10 s)
= 2.1 rad/s2
= (2.1 rad/s2) (360 / (2 π) degrees/rad)
= 120 degrees/s2
Angular Moment - or Torque
Angular moment or torque can be expressed as:
T = α I (2f)
where
T = angular moment or torque (N m)
I = Moment of inertia (lbm ft2, kg m2)
