Pulling an Airplane

The force to move an airplane on an absolute flat runway with no wind at constant low speed is equal to the rolling resistance between the plane and the tarmac.

The rolling resistance for the air plane can be calculated as

F _r = c m _r a _g (1)

where

F _r = rolling resistance (N, lb_f )

c = rolling resistance coefficient

m _r = rolling mass (kg, lb_m )

a _g = acceleration of gravity (9.81 m/s²)

Example - Force required to pull an airplane at constant low speed on tarmac

If the mass of a plane is 40000 kg and the rolling coefficient between the aircraft wheel and the tarmac is 0.02 - the force required to overcome the rolling resistance can be calculated as

F _r = 0.02 (40000 kg) (9.81 m/s²)

= 7848 N

This force can be delivered by a pulling truck or - as occasionally seen - by a number of pulling people. Enough weight for the pullers are required to create friction forces against the tarmac that equals the plane rolling resistance.

The friction force for the puller can be calculated to

F_f = μ W

= μ m_f a _g (2)

where

F_f = frictional force (N, lb)

μ = friction coefficient

W = weight (N, lb_f )

m_f = friction mass (kg)

Example - Required Mass for Pulling Truck

The friction coefficient between a pulling truck rubber wheels and dry tarmac is 0.9. Since pulling trucks are connected to air crafts nose wheels close to tarmac we simplify the calculation of required truck mass to

m_f = (7848 N) / (0.9 (9.81 m/s²) )

= 889 kg

Example - Air Craft Pulled by People

When persons participates in aircraft pulling there is normally an offset between the rope connected to the air craft nose wheel and the tarmac. It is common for persons to bend over with the rope over the shoulder or holding it in the hands.

The horizontal friction force between the persons shoes and the tarmac must be equal or larger than the air plane rolling resistance.  The minimum required vertical force - or minimum weight of the people - depends on the bending angle as illustrated in the vector diagram below.

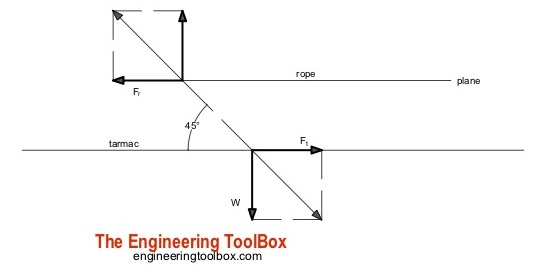
If they bend over 45 ^o - the vertical force or weight equals to the horizontal force. With rubber shoes and the same friction coefficient as above for the truck the weight of the people should be 889 kg . With an average weight of 80 kg/person - the number of persons can be calculated to

n = (889 kg) / (80 kg/person)

= 11.1

= 12

With a more realistic bending angle 60 ^o - the minimum vertical force or weight can be calculated as

W = tan(60 ^o )  (7848 N)

= 13593 N

The minimum mass of people to achieve this weight can be calculated as

m_f = W / a _g

= (13593 N) / (9.81 m/s²)

= 1386 kg

With an average weight of 80 kg/person - the minimum number of persons can be calculated to

n = (1386 kg) (80 kg/person)

= 17.3

= 18