Kirchhoff's Voltage and Current Laws
Kirchhoff's current and voltage laws.
Kirchhoff's Current Law
Also called Kirchhoff's first law, Kirchhoff's point rule, Kirchhoff's junction rule (or nodal rule) or Kirchhoff's first rule.
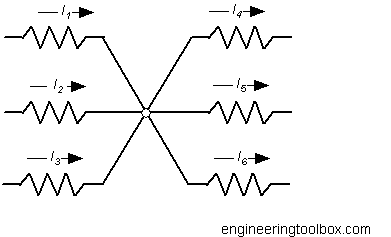
At any junction in an electric circuit the total current flowing towards the junction or node is equal to the total current flowing away from the junction.
Kirchhoff's Current Law can be expressed as
Σ I = I1 + I2 + .. + In = 0 (1)
where
I = currents (amps)
In general - current toward the junction is positive and current flowing away from the junction is negative.
Example - Kirchhoff's Current Law
The currents in the figure above is I1 = 0.1 A, I2 = 0.2 A, I3 = 0.1 A, I4 = - 0.05 A, I5 = -0.15 A.
I6 can be calculated by using Kirchhoff's current law
(0.1 A) + (0.2 A) + (0.1 A) + (- 0.05 A) + (-0.15 A) + I6 = 0
or
I6 = -((0.1 A) + (0.2 A) + (0.1 A) + (- 0.05 A) + (-0.15 A))
= -0.2 A
Kirchhoff's Voltage Law
Also called Kirchhoff's second law, Kirchhoff's loop (or mesh) rule, or Kirchhoff's second rule.
In a closed loop in a network the sum of the voltage drops or potential differences around the loop is zero.
Kirchhoff's Voltage Law can be expressed as
Σ U = U1 + U2 + .. + Un = 0 (2)
where
U = voltage drop or potential difference (volts)
In a schematic diagram voltage can be measured positive clockwise or anticlockwise.
Related Topics
-
Electrical
Electrical engineering with units, amps and electrical wiring. Wire gauges, electrical formulas, motors and more.
Related Documents
-
Current Divider - Online Calculator
An electric current divider outputs a current that is a fraction of the input current. -
Electric Circuit Diagram - Drawing Template
Online shareable electric circuit diagram. -
Electrical Parallel Circuits
Resistance, voltage and current in electrical parallel circuits. -
Electrical Series Circuits
Voltage and current in electrical series circuits. -
Relative vs. Absolute Voltage
Electric circuits and voltage at any point. -
Resistance vs. Resistivity
Electrical resistance and resistivity. -
Voltage Dividers - Online Calculator
Output voltage potential divider. -
Voltage Sources vs. Current Sources
Voltage and Current Sources
