Poisson's Ratio
When a material is stretched in one direction it tends to get thinner in the other two directions.
When a sample of material is stretched in one direction it tends to get thinner in the lateral direction - and if a sample is compressed in one direction it tends to get thicker in the lateral direction.
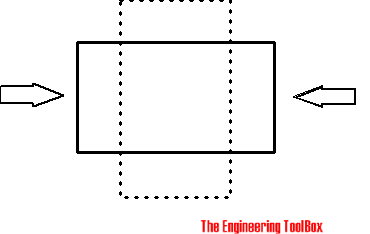
Poisson's ratio is
- the ratio of the relative contraction strain (transverse, lateral or radial strain) normal to the applied load - to the relative extension strain (or axial strain) in the direction of the applied load
Poisson's Ratio can be expressed as
μ = - ε t / ε l (1)
where
μ = Poisson's ratio
ε t = transverse strain (m/m, ft/ft)
ε l = longitudinal or axial strain (m/m, ft/ft)
Strain is defined as "deformation of a solid due to stress".
Longitudinal (or axial) strain can be expressed as
ε l = dl / L (2)
where
ε l = longitudinal or axial strain (dimensionless - or m/m, ft/ft)
dl = change in length (m, ft)
L = initial length (m, ft)
Contraction (or transverse, lateral or radial) strain can be expressed as
ε t = dr / r (3)
where
ε t = transverse, lateral or radial strain (dimensionless - or m/m, ft/ft)
dr = change in radius (m, ft)
r = initial radius (m, ft)
Eq. 1, 2 and 3 can be combined to
μ = - ( dr / r ) / ( dl / L ) (4)
Example - Stretching Aluminum
An aluminum bar with length 10 m and radius 100 mm (100 10-3 m) is stretched 5 mm (5 10-3 m) . The radial contraction in lateral direction can be rearranged to
dr = - μ r dl / L (5)
With Poisson's ratio for aluminum 0.334 - the contraction can be calculated as
dr = - 0.334 ( 100 10-3 m ) ( 5 10-3 m) / (10 m)
= 1.7 10 -5 m
= 0.017 mm
Poisson's Ratios for Common Materials
For most common materials the Poisson's ratio is in the range 0 - 0.5 . Typical Poisson's Ratios for some common materials are indicated below.
| Material | Poisson's Ratio - μ - |
|---|---|
| Upper limit | 0.5 |
| Aluminum | 0.334 |
| Aluminum, 6061-T6 | 0.35 |
| Aluminum, 2024-T4 | 0.32 |
| Beryllium Copper | 0.285 |
| Brass, 70-30 | 0.331 |
| Brass, cast | 0.357 |
| Bronze | 0.34 |
| Clay | 0.41 |
| Concrete | 0.1 - 0.2 |
| Copper | 0.355 |
| Cork | 0 |
| Glass, Soda | 0.22 |
| Glass, Float | 0.2 - 0.27 |
| Granite | 0.2 - 0.3 |
| Ice | 0.33 |
| Inconel | 0.27 - 0.38 |
| Iron, Cast - gray | 0.211 |
| Iron, Cast | 0.22 - 0.30 |
| Iron, Ductile | 0.26 - 0.31 |
| Iron, Malleable | 0.271 |
| Lead | 0.431 |
| Limestone | 0.2 - 0.3 |
| Magnesium | 0.35 |
| Magnesium Alloy | 0.281 |
| Marble | 0.2 - 0.3 |
| Molybdenum | 0.307 |
| Monel metal | 0.315 |
| Nickel Silver | 0.322 |
| Nickel Steel | 0.291 |
| Polystyrene | 0.34 |
| Phosphor Bronze | 0.359 |
| Rubber | 0.48 - ~0.5 |
| Sand | 0.29 |
| Sandy loam | 0.31 |
| Sandy clay | 0.37 |
| Stainless Steel 18-8 | 0.305 |
| Steel, cast | 0.265 |
| Steel, Cold-rolled | 0.287 |
| Steel, high carbon | 0.295 |
| Steel, mild | 0.303 |
| Titanium (99.0 Ti) | 0.32 |
| Wrought iron | 0.278 |
| Z-nickel | 0.36 |
| Zinc | 0.331 |
Related Topics
-
Mechanics
The relationships between forces, acceleration, displacement, vectors, motion, momentum, energy of objects and more. -
Miscellaneous
Engineering related topics like Beaufort Wind Scale, CE-marking, drawing standards and more.
Related Documents
-
Malleability vs. Brittlenes vs. Ductility
Plastic deformation properties. -
Metals - Machinability
The machinability of some common metals. -
Metals and Alloys - Bulk Modulus Elasticity
The Bulk Modulus - resistance to uniform compression - for some common metals and alloys. -
Metals and Alloys - Young's Modulus of Elasticity
Elastic properties and Young's modulus for metals and alloys like cast iron, carbon steel and more. -
Modulus of Rigidity
Shear Modulus (Modulus of Rigidity) is the elasticity coefficient for shearing or torsion force. -
Poisson's Ratios Metals
Some metals and their Poisson's Ratios. -
Ratios and Proportions
The relative values between quantities - ratios and proportions. -
Stress, Strain and Young's Modulus
Stress is force per unit area - strain is the deformation of a solid due to stress. -
Young's Modulus, Tensile Strength and Yield Strength Values for some Materials
Young's Modulus (or Tensile Modulus alt. Modulus of Elasticity) and Ultimate Tensile Strength and Yield Strength for materials like steel, glass, wood and many more.




