Moist Air - Density vs. Water Content and Temperature
Density of the mix of dry air and water vapor - moist humid air.
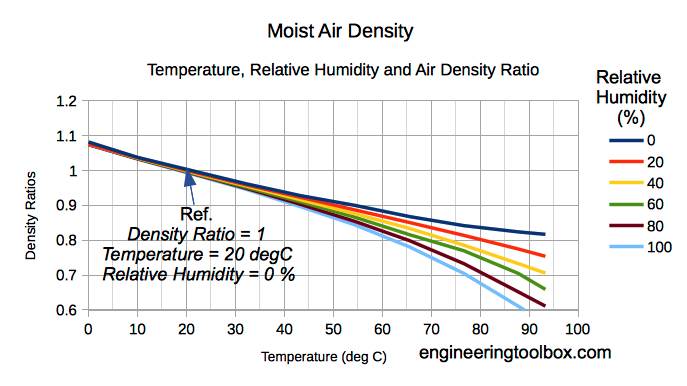
The density of humid air varies with water content and temperature. When the temperature increases a higher molecular motion results in expansion of volume and a decrease of density.
The density of a gas, dry air, water vapor - or a mixture of dry air and water vapor like moist or humid air - can be calculated with the Ideal Gas Law .
Density of Dry Air
The density of dry air can be calculated
ρ a = p a / R a T
= 0.0035 p a / T (1)
where
ρ a = density dry air (kg/m3 )
p a = partial pressure of dry air (Pa, N/m2)
R a = 286.9 - individual gas constant of dry air (J/kg K)
T = absolute dry bulb temperature (K)
Density of Water Vapor
The density of the water vapor can be calculated
ρ w = p w / R w T
= 0.0022 p w / T (2)
where
p w = partial pressure of water vapor (Pa, N/m2)
ρ w = density of water vapor (kg/m3 )
R w = 461.5 - individual gas constant water vapor (J/kg K)
T = absolute dry bulb temperature (K)
Density of Moist Air - an Air Vapor Mixture
The amount of water vapor in air influences the density. Water vapor is relatively light compared to diatomic Oxygen and diatomic Nitrogen - the dominant components in air .
When vapor content increases in moist air the amount of Oxygen and Nitrogen are decreased per unit volume and the density of the mix decreases since the mass is decreasing.
Based on specific volume of moist air the moist air density can be calculated
ρ = 1 / v
= (p / R a T) (1 + x) / (1 + x R w / R a ) (3)
where
v = specific volume of moist air per mass unit of dry air and water vapor (m3 /kg)
x = m w / m a = specific humidity or humidity ratio (kg h2o /kg dry_air )
m w = mass of water vapor (kg)
m a = mass of dry air (kg)
p = pressure in the moist air (Pa)
The density of dry air with the same total pressure p as in the mixture (dry air + vapor partial pressure) - can be calculated as a reference as
ρ ref = p / R a T (4)
where
ρ ref = reference density of dry air with the same pressure as in the air vapor mixture (kg/m3 )
The density of moist air related to dry air can be expressed by combining (4) and (3) as
ρ = ρ ref (1 + x) / (1 + x R w / R a ) (5)
The gas constant ratio between water vapor and air is
R w / R a = (461.5 J/kg K) / (286.9 J/kg K)
= 1.609
and inserting the ratio in (5) the density of moist air related to dry air can be expressed as
ρ = ρ ref (1 + x) / (1 + 1.609 x ) (6)
Note! As we can see from (6) - increased moisture content reduces the density of moist air - dry air is more dense than moist air.
Related Topics
-
Air Psychrometrics
Moist and humid air calculations. Psychrometric charts and Mollier diagrams. Air-condition systems temperatures, absolute and relative humidities and moisture content in air. -
Densities
Densities of solids, liquids and gases. Definitions and convertion calculators. -
Gases and Compressed Air
Properties of air, LNG, LPG and other common gases. Pipeline capacities and sizing of relief valves.
Related Documents
-
Air - Composition and Molecular Weight
Dry air is a mechanical mixture of nitrogen, oxygen, argon and several other gases in minor amounts. -
Air - Humidifying by Adding Steam or Water
Air can be humidified by adding water or steam. -
Air - Humidifying with Steam - Imperial Units
Estimate the amount of steam required (lb/h in 100 cfm) in humid air. -
Air - Humidifying with Steam, SI units
Using steam to humidify air. -
Air - Humidity Measurement from Dry and Wet Bulb Temperature
Relative humidity in moist air can estimated by measuring the dry and wet bulb temperature. -
Air - Humidity Ratio
The mass of water vapor present in moist air - to the mass of dry air. -
Air - Maximum Moisture Carrying Capacity
Maximum water content in humid air vs. temperature. -
Air - Moisture Holding Capacity vs. Temperature
The moisture holding capacity of air increases with temperature. -
Air - Molecular Weight and Composition
Dry air is a mixture of gases where the average molecular weight (or molar mass) can be calculated by adding the weight of each component. -
Air and Steam Mixtures
Air in the steam will lower the surface temperatures in heat exchangers - and less heat will be transferred. -
Dry Air - Thermodynamic and Physical Properties
Thermodynamic properties of dry air - specific heat, ratio of specific heats, dynamic viscosity, thermal conductivity, Prandtl number, density and kinematic viscosity at temperatures ranging 175 - 1900 K. -
Dry Air and Water Vapor - Density and Specific Volume vs. Temperature - Imperial Units
Density and specific volume of dry air and water vapor at temperatures ranging 225 to 900 degF (107 to 482 degC). -
Humid Air vs. the Ideal Gas Law
Pressure, temperature and volume in a perfect ideal gas like moist air (air with water vapor). -
Mixing of Humid Air
The change in state wwhen mixing moist air - enthalpy, heat, temperature and specific humidity. -
Moist Air - Daltons Law of Partial Pressure
The pressure in a mixture of dry air and water vapor - humid or moist air - can be estimated by using Daltons Law of partial pressures. -
Moist Air - Degree of Saturation
Humidity ratio of moist air to humidity ratio of saturated moist air. -
Moist Air - Density vs. Pressure
Density of moist air vs. pressure ranging 75 - 1000 mmHg. -
Moist Air - Psychrometric Table for Pressure 29.92 inHg
Dry and wet bulb temperatures, saturation pressure, water vapor weight, specific volume, heat and more. -
Moist Air - Specific Volume
Specific volume of moist air is defined as the total volume of humid air per mass unit of dry air -
Moist Air - Specific vs. Relative Humidity
Specific humidity of moist air vs. relative humidity, water vapor and air density. -
Moist Air - Water Vapor and Saturation Pressure
Saturation pressure of water vapor in moist air vs. temperature. -
Moist Air - Weight of Water Vapor
Weight of water vapor in air -
Saturated Salt Solutions - Controlling Air Humidity
A salt solutions can be used maintain a particular value of relative humidity. -
Wet Steam - Specific Volume
Wet steam and specific volume.




