Stress
Stress is force applied on cross-sectional area.
Stress is the ratio between applied force and cross-sectional area where the applied force is acting.
Normal Stress
Normal stress can be expressed as
σ = FN / A (1)
where
σ = normal stress (N/m2, Pa, psi)
FN = applied force perpendicular to the area - Normal force (N, lb)
A = cross-sectional area (m2, in2)
Shear Stress
Shear stress can be expressed as
τ = FV / A (2)
where
τ = shear stress (N/m2, Pa, psi)
FV = applied force in plane of the area - Shear force (N, lb)
Example - Normal Stress in a Column
A 10000 N force is acting in the direction of a British Universal Column UB 152 x 89 x 16 with cross sectional area 20.3 cm2. The normal stress in the column can be calculated as
σ = (10000 N) / ((20.3 cm2) (0.0001 m2/cm2))
= 4926108 Pa (N/m2)
= 4.9 MPa
The Yield strength - the amount of stress that a material can undergo before moving from elastic deformation into plastic deformation - is typical 250 MPa for steel.
Example - Shear Stress in a Beam with Point Load
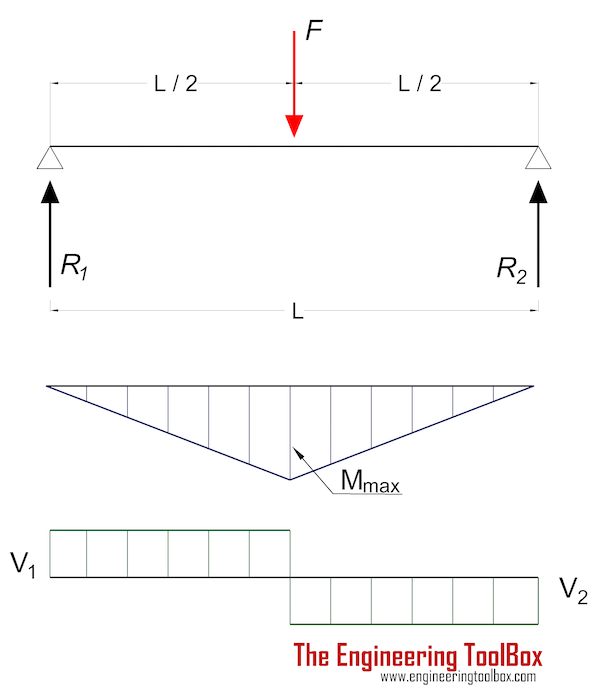
For a beam with single point load supported on both ends - the shear force Fv (or V in the figure above) is equal in magnitude to support force R1 or R2.
Reaction forces can be calculated due to moment equilibrium around support 1
F L / 2 = R2 L (4)
R2 = F / 2 (5)
R1 = R2
= F / 2 (6)
For a 10000 N point load perpendicular on a beam similar to the example above - supported at both ends - the magnitude of the reaction and shear forces can be calculated as
R1 = R2
= V1
= V2
= (10000 N) / 2
= 5000 N
= 5 kN
The shear stress can be calculated as
τ = (5000 N) / ((20.3 cm2) (0.0001 m2/cm2))
= 2463054 Pa
= 2.5 MPa



