Stress in Thin-Walled Cylinders or Tubes
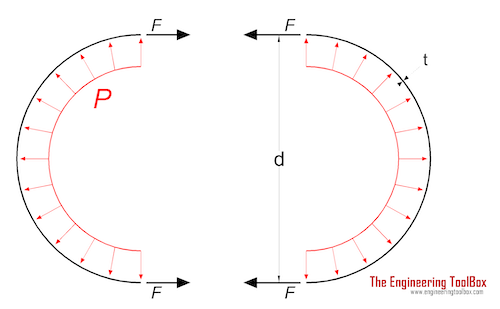
Hoop and longitudinal stress thin-walled tubes or cylinders.
When a thin-walled tube or cylinder is subjected to internal pressure a hoop and longitudinal stress are produced in the wall.
For the thin walled equations below the wall thickness is less than 1/20 of tube or cylinder diameter.
Hoop (Circumferential) Stress
The hoop stress is acting circumferential and perpendicular to the axis and the radius of the cylinder wall. The hoop stress can be calculated as
σh = p d / (2 t) (1)
where
σh = hoop stress (MPa, psi)
p = internal pressure in the tube or cylinder (MPa, psi)
d = internal diameter of tube or cylinder (mm, in)
t = tube or cylinder wall thickness (mm, in)
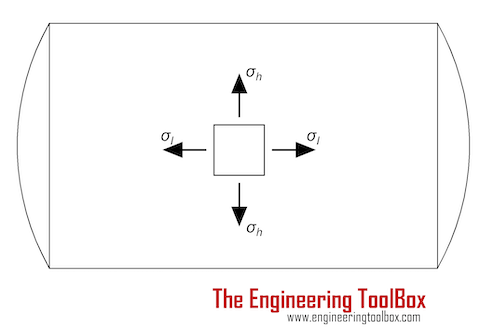
Longitudinal (Axial) Stress
For a cylinder closed closed in both ends the internal pressure creates a force along the axis of the cylinder. The longitudinal stress caused by this force can be calculated as
σl = p d / (4 t) (2)
where
σl = longitudinal stress (MPa, psi)
Example - Stress in a Thin Walled Tube
The pressure in a thin walled tube with diameter 0.3 m and thickness 0.001 m is 1000 kPa (10 bar).
The hoop stress can be calculated
σh = (1000 kPa) (0.3 m) / (2 (0.001 m))
= 150000 kPa
= 150 MPa
The longitudinal stress can be calculated
σh = (1000 kPa) (0.3 m) / (4 (0.001 m))
= 75000 kPa
= 75 MPa
Note that typical maximum allowable stress for carbon steel pipes is below 135 MPa.
Related Topics
-
Mechanics
The relationships between forces, acceleration, displacement, vectors, motion, momentum, energy of objects and more. -
Statics
Forces acting on bodies at rest under equilibrium conditions - loads, forces and torque, beams and columns.
Related Documents
-
Fixed Pipes - Stress vs. Change in Temperature
Temperature changes introduces stress fixed pipes. -
Process Pipes - Allowable Stress vs. Temperature
Allowable wall stress in pipes according ASME M31.3. -
Rotating Bodies - Stress
Stress in rotating disc and ring bodies. -
Rotating Shafts - Torque
Torsional moments acting on rotating shafts. -
Stress
Stress is force applied on cross-sectional area. -
Stress in Thick-Walled Cylinders or Tubes
Radial and tangential stress in thick-walled cylinders or tubes with closed ends - with internal and external pressure. -
Stress, Strain and Young's Modulus
Stress is force per unit area - strain is the deformation of a solid due to stress.