Speed of Sound - Equations
Calculate the speed of sound (the sonic velocity) in gases, fluids or solids.
A disturbance introduced in some point of a substance - solid or fluid - will propagate through the substance as a wave with a finite velocity.
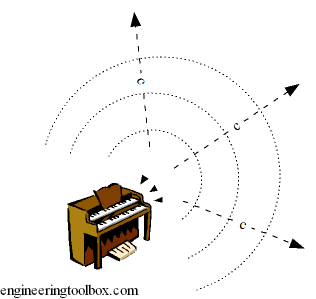
Acoustic Velocity and Speed of Sound
The velocity at which a small disturbance will propagate through the medium is called Acoustic Velocity or Speed of Sound.
Note that speed is a scalar quantity. Velocity is vector quantity with direction.
The acoustic velocity is related to the change in pressure and density of the substance and can be expressed as
c = (dp / dρ)1/2 (1)
where
c = speed of sound (m/s, ft/s)
dp = change in pressure (Pa, psi)
dρ = change in density (kg/m3, lb/ft3)
Speed of Sound in Gases, Fluids and Solids
The acoustic velocity can alternatively be expressed with Hook's Law as
c = (K / ρ)1/2 (2)
where
K = Bulk Modulus of Elasticity (Pa, psi)
ρ = density (kg/m3, lb/ft3)
This equation is valid for liquids, solids and gases. The sound travels faster through media with higher elasticity and/or lower density. If a medium is not compressible at all - incompressible - the speed of sound is infinite (c ≈ ∞).
| Substance | Bulk Modulus Elasticity - K - (109 N/m2) | Density - ρ - (kg/m3) |
|---|---|---|
| Water (10oC) | 2.09 | 999.7 |
| Oil | 1.35 | 920 |
| Ethyl Alcohol | 1.06 | 810 |
| Mercury | 28.5 | 13595 |
- properties at 1 bar and 0 oC
Speed of Sound - Sonic Velocity - in Ideal Gases
Since the acoustic disturbance introduced in a point is very small the heat transfer can be neglected and for gases assumed isentropic. For an isentropic process the ideal gas law can be used and the speed of sound can be expressed as
c = (k p / ρ)1/2
= (k R T)1/2 (3)
where
k = ratio of specific heats (adiabatic index)
p = pressure (Pa, psi)
R = individual gas constant(J/kg K, ft lb/slug oR)
T = absolute temperature (oK, oR)
For an ideal gas the speed of sound is proportional to the square root of the absolute temperature.
Example - Speed of Sound in Air
The speed of sound in air at 0 oC (273.15 K) and absolute pressure 1 bar can be calculated as
c = (1.4 (286.9 J/K kg) (273.15 K))1/2
= 331.2 (m/s)
where
k = 1.4
and
R = 286.9 (J/K kg)
The speed of sound in air at 20 oC(293.15 K) and absolute pressure 1 bar can be calculated as
c = (1.4 (286.9 J/K kg) (293.15 K))1/2
= 343.1 (m/s)
Example - Speed of Sound in Water
The speed of sound in water at 10 oC can be calculated as
c = ((2.09 109 N/m2) / (999.7 kg/m3))1/2
= 1446 (m/s)
where
Ev= 2.09 109 (N/m2)
and
ρ = 999.7 (kg/m3)
- Speed of Sound in Water - Speed of sound in water at different temperatures - imperial and SI units.
Speed of Sound in Solids
- Speed of Sound in common Solids
- Elastic Properties and Young Modulus for some Materials
- The Bulk Modulus for Elasticity
- Material Properties
Subsonic and Supersonic speed
- If the Mach Number is below 1, the flow velocity is lower than the speed of sound - and the speed is subsonic.
- If the Mach Number is 1 - the speed is transonic.
- If the Mach Number is above 1, the flow velocity is higher than the speed of sound - and the speed is supersonic.
Related Topics
-
Acoustics
Room acoustics and acoustic properties. decibel A, B and C calculations. Noise Rating (NR) curves. Sound transmission through walls. Calculate sound pressure, sound intensity and sound attenuation. -
Fluid Mechanics
The study of fluids - liquids and gases. Involving velocity, pressure, density and temperature as functions of space and time.
Related Documents
-
Acetone - Thermophysical Properties
Chemical, physical and thermal properties of acetone, also called 2-propanone, dimethyl ketone and pyroacetic acid. Phase diagram included. -
Air - Speed of Sound vs. Temperature
Speed of sound in air at standard atmospheric pressure with temperatures ranging -40 to 1000 °C (-40 to 1500 °F) - Imperial and SI Units. -
Benzene - Thermophysical properties
Chemical, physical and thermal properties of benzene, also called benzol. Phase diagram included. -
Bulk Modulus and Fluid Elasticities
Introduction to - and definition of - Bulk Modulus Elasticity commonly used to characterize the compressibility of fluids. -
Ethylene - Thermophysical Properties
Chemical, physical and thermal properties of ethylene, also called ethene, acetene and olefiant gas. Phase diagram included. -
Gases - Ratios of Specific Heat
Ratios of specific heat for gases with constant pressure and volume processes. -
Gases - Speed of Sound
Speed of sound in some gases at zero degrees Celsius and atmospheric pressure. -
Hooke's Law
Hooke's law - force, elongation and spring constant. -
International Standard Atmosphere
International standard atmosphere in elevation -2000 to 30000 metre - pressure, temperature, density, viscosity, thermal conductivity and velocity of sound. -
Isentropic Flow
Fluid flow with constant entropy is also called isentropic flow. -
Liquids - Speed of Sound
Speed of sound in common fluids like water, glycerol, kerosene and more. -
Mach Number
An introduction to the Mach Number. -
Maximum Sound Pressure Levels in Rooms
Maximum recommended sound pressure levels in rooms like kindergartens, auditoriums, libraries, cinemas and more. -
Solids and Metals - Speed of Sound
Speed of sound in solids and metals like aluminum, brass, concrete and more. -
Sound - Abatement vs. the Distance from Source
The disruption of the sound pressure wave and the reduction of noise is called attenuation - Sound Pressure Level vs. distance calculator. -
Sound - Attenuation and Speed vs. Sound Frequency and Air Humidity
The speed and attenuation of sound in moist air varies with sound frequency and air humidity. -
Speed of Sound vs. Elevation, Temperature and Air Pressure
Altitude and speed of sound, temperature and pressure. -
Velocity Units Converter
Convert between speed and velocity units like m/s, km/h, knots, mph and ft/s. -
Water - Speed of Sound vs. Temperature
Speed of sound in water at temperatures ranging 32 - 212°F (0 - 100°C) - Imperial and SI units. -
Young's Modulus, Tensile Strength and Yield Strength Values for some Materials
Young's Modulus (or Tensile Modulus alt. Modulus of Elasticity) and Ultimate Tensile Strength and Yield Strength for materials like steel, glass, wood and many more.




