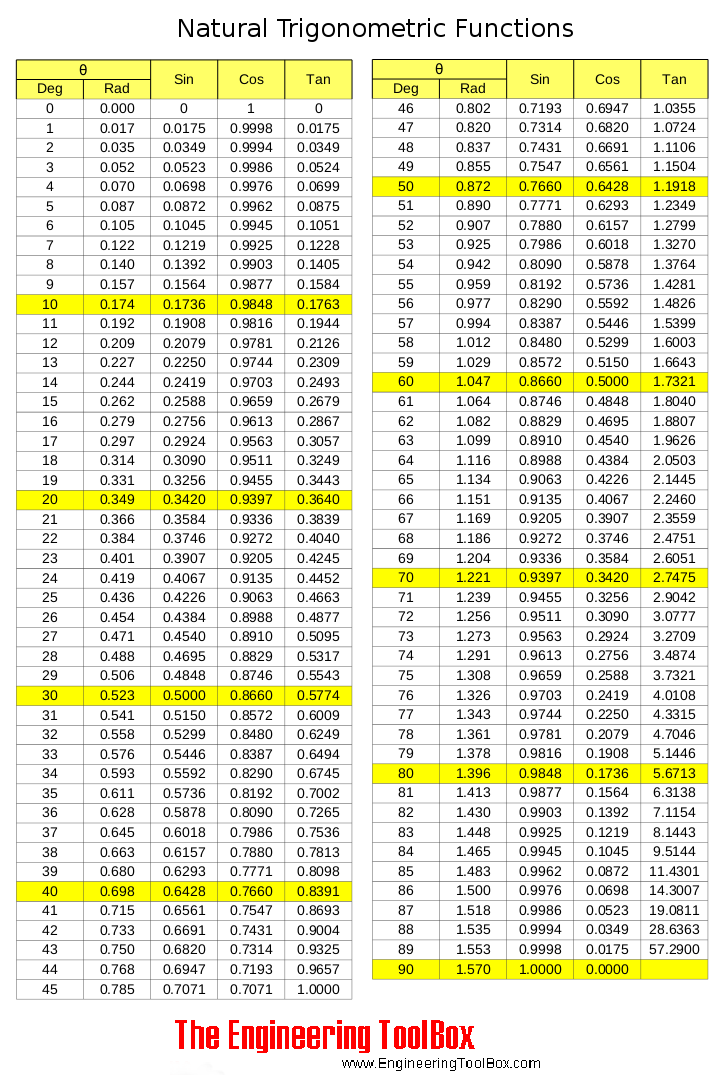
Trigonometric Functions
Sine, cosine and tangent - the natural trigonometric functions.
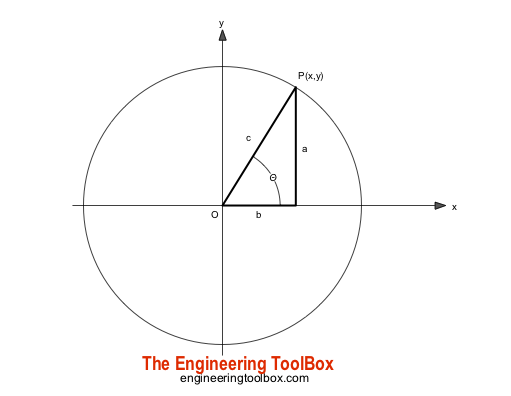
Natural trigonometric functions are expressed as
sin(θ d ) = a / c
= 1 / csc( θ d )
= cos(π / 2 - < θ r < ) (1)
where
θ d = angle in degrees
θ r = angle in radians
cos( θ d ) = b / c
= 1 / sec( θ d )
= sin(π / 2 - θ r ) (2)
tan( θ d ) = a / b
= 1 / cot( θ d )
= sin( θ d ) / cos( θ d )
= cot(π / 2 - θ r ) (3)
cot( θ d ) = 1 / tan( θ d )
= cos( θ d ) / sin( θ d )
= tan(π / 2 - θ r ) (4)
Trigonometric functions ranging 0 to 90 degrees are tabulated below:
Inverse functions
arcsin (a) = sin-1 (a) (1a)
arccos (a) = cos-1 (a) (2a)
arctan (a) = tan-1 (a) (3a)
Addition Formula
sin (a ± b) = sin (a) cos (b) ± cos (a) sin (b) (5)
cos (a ± b) = cos (a) cos (b) ± sin (a) sin (b) (5b)
tan (a ± b) = (tan(a) ± tan(b)) / (1 ± tan(a) tan(b)) (5c)
Sum and Difference Formula
sin (a) + sin (b) = 2 sin ((a + b)/2) cos ((a + b)/2) (6)
sin (a) - sin (b) = 2 cos ((a + b)/2) sin ((a - b)/2) (6b)
cos (a) + cos (b) = 2 cos ((a + b)/2) cos ((a - b)/2) (6c)
cos (a) - cos (b) = - 2 sin ((a + b)/2) sin ((a - b)/2) (6d)
tan (a) + tan (b) = sin (a + b) / (cos (a) cos (b)) (6e)
tan (a) - tan (b) = sin (a - b) / (cos (a) cos (b)) (6f)
Product Formula
2 sin (a) cos (b) = sin (a - b) + sin (a + b) (7)
2 sin (a) sin (b) = cos (a - b) - cos (a - b) (7b)
2 cos (a) cos (b) = cos (a - b) + cos (a + b) (7c)
Multiple Angle and Powers Formula
sin (2 a) = 2 sin (a) cos (a) (8)
cos (2 a) = cos2(a) - sin2(a) (8b)
cos (2 a) = 2 cos2(a) - 1 (8c)
cos (2 a) = 1 - 2 sin2(a) (8d)
tan (2 a) = 2 tan a / (1 - tan2(a)) (8e)
sin2(a) + cos2(a) = 1 (8f)
sec2(a) = tan2(a) + 1 (8g)
Special Triangles
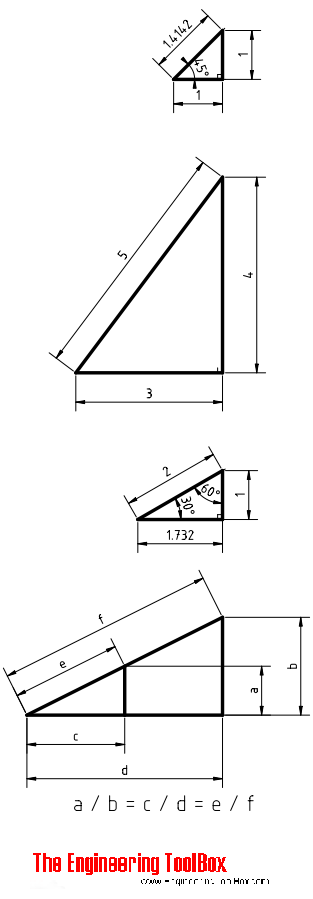
Trigonometric Values
sin(-θ d ) = - sin(θ d ) (9a)
where
θ d = angle in degrees
sin(90° + θ d ) = cos(θ d ) (9b)
sin(90° - θ d ) = cos(θ d ) (9c)
sin(180° + θ d ) = - sin(θ d ) (9d)
sin(180° - θ d ) = sin(θ d ) (9e)
sin(270° + θ d ) = - cos(θ d ) (9f)
sin(270° - θ d ) = - cos(θ d ) (9g)
sin(360° + θ d ) = sin(θ d ) (9h)
sin(360° - θ d ) = - sin(θ d ) (9h)
cos(-θ d ) = cos(θ d ) (10a)
cos(90° + θ d ) = - sin(θ d ) (10b)
cos(90° - θ d ) = sin(θ d ) (10c)
cos(180° + θ d ) = - cos(θ d ) (10d)
cos(180° - θ d ) = - cos(θ d ) (10e)
cos(270° + θ d ) = sin(θ d ) (10f)
cos(270° - θ d ) = - sin(θ d ) (10g)
cos(360° + θ d ) = cos(θ d ) (10h)
cos(360° - θ d ) = cos(θ d ) (10h)
tan(-θ d ) = - tan(θ d ) (11a)
tan(90° + θ d ) = - cot(θ d ) (11b)
tan(90° - θ d ) = cot(θ d ) (11c)
tan(180° + θ d ) = tan(θ d ) (11d)
tan(180° - θ d ) = - tan(θ d ) (11e)
tan(270° + θ d ) = - cot(θ d ) (11f)
tan(270° - θ d ) = cot(θ d ) (11g)
tan(360° + θ d ) = tan(θ d ) (11h)
tan(360° - θ d ) = - tan(θ d ) (11h)
Trigometric Functions of Common Angles
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| Sin | 0 | 1 / 2 | √2 / 2 | √3 / 2 | 1 |
| Cos | 1 | √2 / 2 | √2 / 2 | 1 / 2 | 0 |
| Tan | 0 | √3 / 3 | 1 | √3 | ∞ |
| Cot | ∞ | √3 | 1 | √3 / 3 | 0 |
| Sec | 1 | 2 √3 / 3 | √2 | 2 | ∞ |
| Cosec | ∞ | 2 | √2 | 2 √3 / 3 | 1 |
Related Topics
-
Basics
Basic engineering data. SI-system, unit converters, physical constants, drawing scales and more. -
Mathematics
Mathematical rules and laws - numbers, areas, volumes, exponents, trigonometric functions and more.
Related Documents
-
Algebraic Expressions
Principal algebraic expressions formulas. -
Angle Calculator - Carpenter's Square
Calculate angles with a straight board across carpenter's square. -
Angle Converter
Converting between angle units. -
Centroids of Plane Areas
The controid of square, rectangle, circle, semi-circle and right-angled triangle. -
Complex Numbers
Complex numbers are used in alternating current theory and mechanical vector analysis. -
Fractions
Law of fractions -
Geometric Shapes - Areas
Areas, diagonals and more - of geometric figures like rectangles, triangles, trapezoids .. -
Hyperbolic Functions
Exponential functions related to the hyperbola. -
Law of Cosines
One side of a triangle when the opposite angle and two sides are known. -
Law of Tangents
Triangles and law of tangents. -
Laws of Indices
Simplifying calculations by involving indices. -
Logarithms
The rules of logarithms - log10 and loge for numbers ranging 1 to 1000. -
Miter Saw - Calculate Sawing Angle
Calculate miter saw protractor angles for skirting and decorative mouldings work. -
Numbers - Square, Cube, Square Root and Cubic Root Calculator
Calculate square, cube, square root and cubic root. Values tabulated for numbers ranging 1 to 100. -
Numbers - Squares, Cubes and Roots
Numbers - squares, cubes, square roots and cube roots. -
Oblique Triangle
Calculate oblique triangles. -
Pythagorean Theorem
Verifying square corners. -
Radians vs. Degrees
Radian is the SI unit of angle. Convert between degrees and radians. Calculate angular velocity. -
Right Angled Triangle
Right angled triangle equations. -
Soil - Earth Weight and Composition
Typical weight and composition of soil. -
Squaring with Diagonal Measurements
A rectangle is square if the lengths of both diagonals are equal. -
Standard Differentials and Integrals
Equations for differentials and integrals. -
Taylor Series
Function as an infinite sum of terms. -
Vector Addition
Online vector calculator - add vectors with different magnitude and direction - like forces, velocities and more.