Complex Numbers
Complex numbers are used in alternating current theory and mechanical vector analysis.
There are two main forms of complex numbers
- Cartesian
- Polar
Complex numbers on the Cartesian form
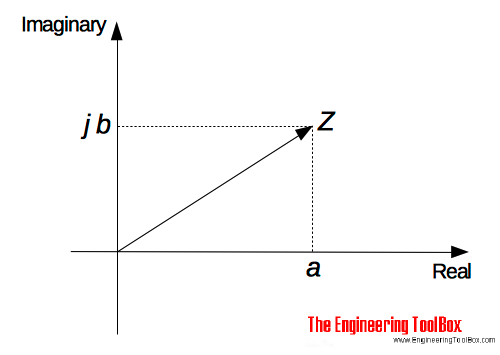
A complex number consists of a real part and an imaginary part and can be expressed on the Cartesian form as
Z = a + j b (1)
where
Z = complex number
a = real part
j b = imaginary part (it is common to use i instead of j)
A complex number can be represented in a Cartesian axis diagram with an real and an imaginary axis - also called the Argand diagram:
Example - Complex numbers on the Cartesian form
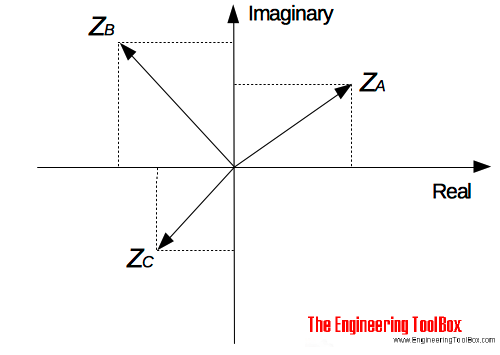
The complex numbers
ZA = 3 + j 2 (2a)
ZB = -3 + j 3 (2b)
ZC = -2 - j 2 (2c)
can be represented in the Argand diagram:
Addition and Subtraction of Complex numbers
Complex numbers are added/subtracted by adding/subtracting the separately the real parts and the imaginary parts of the number.
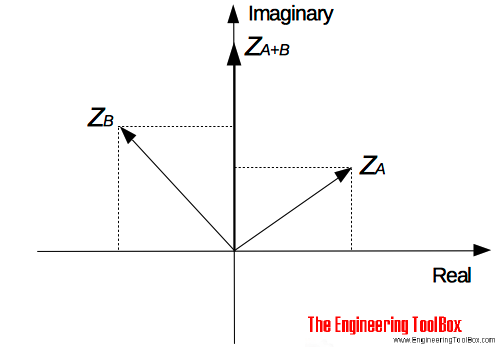
Example - Adding two Complex numbers
ZA = 3 + j 2
ZB = -3 + j 3
Z(A+B) = (3 + (-3)) + (j 2 + j 3)
= j 5
Complex numbers on the Polar form
A complex number on the polar form can be expressed as
Z = r (cosθ + j sinθ) (3)
where
r = modulus (or magnitude) of Z - and is written as "mod Z" or |Z|
θ = argument (or amplitude) of Z - and is written as "arg Z"
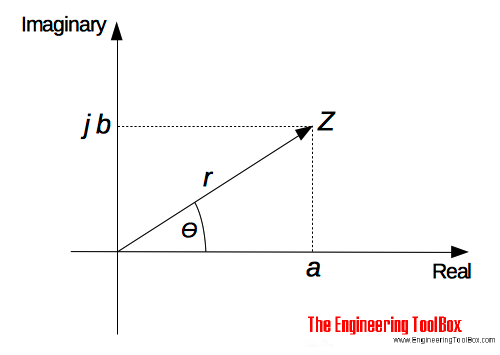
r can be determined using Pythagoras' theorem
r = (a2 + b2)1/2 (4)
θ can be determined by trigonometry
θ = tan-1(b / a) (5)
(3) can also be expressed as
Z = r ej θ (6)
As we can se from (1), (3) and (6) - a complex number can be written in three different ways.
Example - Complex number on the Polar form
The complex number
Za = 3 + j 2
can be expressed on the polar form by calculating the modulus and the argument.
The "modulus" can be calculated by using eq. (4):
r = (32 + 22)1/2
= 3.606
The "argument" can be calculated by using eq. (5):
θ = tan-1(2 / 3)
= 33.69o
The complex number on polar form (3):
Za = 3.606 (cos(33.69) + j sin(33.69))
Or alternatively (6)
Za = 3.606 ej 33.69
Adding or Subtraction of Complex Numbers
Adding Complex Numbers
Za = a + j b
Zb = c + j d
Za + Zb = (a + j b) + (c + j d)
= (a + c) + j(b + d) (6)
or alternative
Za = ra (cosθa + j sinθa)
Zb = rb (cosθb + j sinθb)
Za + Zb = ra (cosθa + j sinθa) + rb (cosθb + j sinθb)
= (ra cosθa + rb cosθb) + j (ra sinθa + rb sinθb) (6b)
or alternatively
Za = ra ejθa
Zb = rb ejθb
Za + Zb = ra ejθa + rb ejθb
= (ra cosθa + rb cosθb) + j (ra sinθa + rb sinθb) (6c)
Example - Adding Complex Numbers
Za = 3 + j 2
Zb = 5 - j 4
Za + Zb = (3 + j 2) + (5 - j 4)
= (3 + 5) + j(2 + (-4))
= 8 - j 2
Example - Adding Complex Numbers
Za = 3 (cos 35 + j sin 35)
Zb = 2 (cos 15 + j sin 15)
Za + Zb = (3 cos 35+ 2 cos 15) + j (3 sin 35 + 2 sin 15)
= 4.38 - j 2.2
Subtracting Complex Numbers
Za = a + j b
Zb = c + j d
Za - Zb = (a + j b) - (c + j d)
= (a - c) + j(b - d) (7)
Example - Subtracting Complex Numbers
Za = 3 (cos 35 + j sin 35)
Zb = 2 (cos 15 + j sin 15)
Za - Zb = 3 (cos 35 + j sin 35) - 2 (cos 15 + j sin 15)
= (3 cos 35 - 2 cos 15) + j (3 sin 35 - 2 sin 15)
= 0.52 + j 1.2
Multiplication of Complex Numbers
Za = a + j b
Zb = c + j d
Za Zb = (a + j b) (c + j d)
= a c + a (j d) + (j b) c + (j b) (j d)
= a c + j a d + j b c + j2 b d (8)
Since j2 = -1 - (8) can be transformed to
Za Zb = (a + j b) (c + j d)
= (a c - b d) + j (a d + b c) (8b)
Example - Multiplying Complex Numbers
Za = 3 + j 2
Zb = 5 - j 4
Za Zb = (3 + j 2) (5 - j 4)
= (3 5 - 2 (-4)) + j(3 (-4) + 2 5)
= 23 - j 2
Complex Conjugate
The complex conjugate of (a + jb) is (a - jb).
Multiplying a complex number with its complex conjugate results in a real number like
Za = a + jb
Za* = a - jb
Za Za* = (a + jb) (a - jb)
= a2 - j a b + j a b - j2 b2
= a2 - (- b2)
= a2 + b2 (9)
Example - Multiplying a Complex Number with its Conjugate
Za = 3 + j 2
Za* = 3 - j 2
Za Za* = (3 + j 2) (3 - j 2)
= 32 + 22
= 13
Division of Complex Numbers
Division of complex numbers can be done with the help of the denominators conjugate:
Za = a + jb
Zb = c + j d
Za / Zb = (a + j b) / (c + j d)
= ((a + j b) / (c + j d)) ((c - j d) / (c - j d))
= (a c + j a d + j b c + j2 b d) / (c2 + d2) (10)
Multiplying both the nominator and the denominator with the conjugate of the denominator is called rationalizing.
