Hydrocarbon Mixtures - Molecular Weight vs. Gravity and Average Boiling Point
Formulas and examples of calculation of average molecular weight of hydrocarbon mixtures from gravity and average boiling point, achieved from distillation data.
For many purposes in chemical engineering, there is important to know the molecular weight (MW) of the fluids in process streams, and for mixtures of several different compounds an average molecular weight can be useful. But, exact analysis of the composition of complex mixtures of hydrocarbons, such as crude oil or oil distillation fractions, which can consist of several thousand different compounds, is difficult to get. Direct measurement of molecular weight is time demanding and gives imprecise results. However, there are several models calculating average molecular weight , based on gravity and distillation data . Two of the most used models, recommended by API, are given below:
Riazi-Daubert 1980: MW = 4.5673E-05 * T R 2.1962 * S -1.0164 (1)
or MW = 1.6607E-04 * T K 2.1962 * S -1.0164 (2)
Riazi-Daubert extended: MW = 20.486 * T R 1.26007 * S 4.98308 * e (1.165E-04*T R -7.78712*S +1.1582E-03*T R *S) (3)
or MW = 42.965 * T K 1.26007 * S 4.98308 * e (2.097E-04*T K -7.78712*S+2.08476E-03*T K *S) (4)
Where
T R = MeABP (mean average boiling point) , in °R (degree Rankin )
T K = MeABP (mean average boiling point) , in K (degree Kelvin )
S = Specific gravity at 60 °F (= 15.6°C)
Equation (1) and (2) fail to properly predict properties for hydrocarbons above C 25 , with boiling point > 400°C (750°F). For heavier oil samples equation (3) and (4) are recommended. These relationships are valid in the ranges:
Molweight: 70 to 700 kg/kmol
MeABP: 20 - 560°C (90 to 1050 °F)
API: 14° to 93°
Specific gravity: 0.630 to 0.973
The average error is said to be about 7%.
Eq. (2) and (4) are used to calculate the molecular weight for a number of specific gravities and boiling points and the results, given with °C and °F, are shown in the figures below
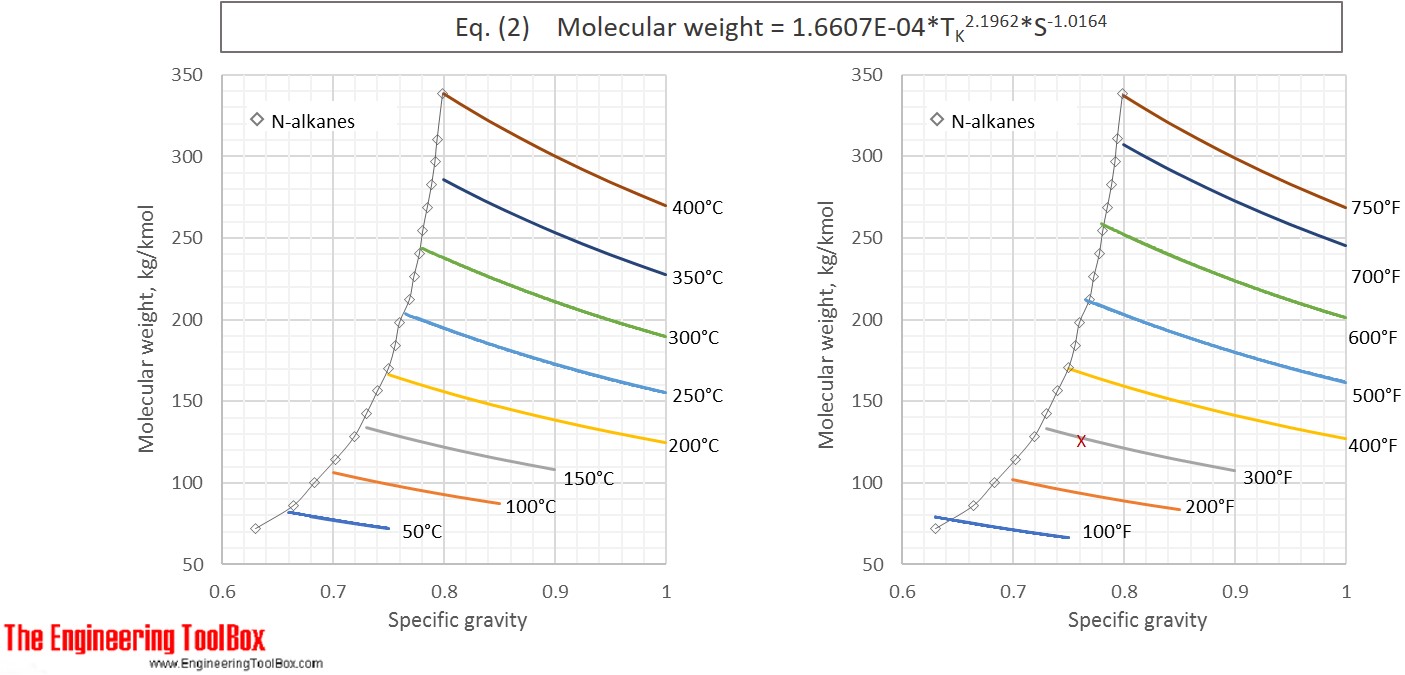
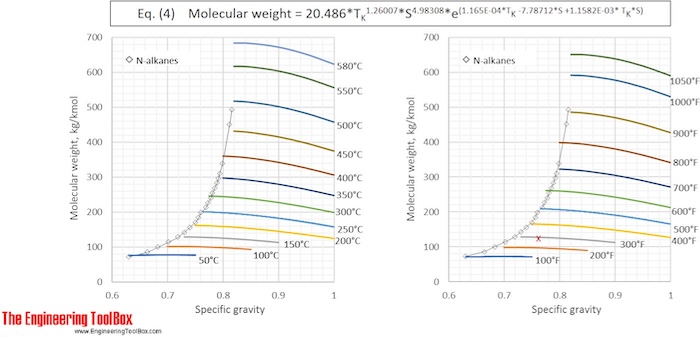
See also Average boiling point from gravity and molecular weight and Molecular Weight - Gases and Vapors
Example 1: Molecular weight of naphtha
Calculate the molecular weight of a naphtha with specific gravtity, S = 0.763 and a MeABP of 292°F
Naphtha is in the low boiling point range, and equation (1) can be applied.
First, °F are converted to °R:
MeABP = 292°F + 460 = 752°R
Average MW = 4.5673E-05 * 752 2.1962 * 0.763 -1.0164 = 124.6 kg/kmol
Applying equation (3) gives
Average MW = 20.486 * 752 1.26007 * 0.763 4.98308 * e (1.165E-04*752 -7.78712*0.763 +1.1582E-03*752*0.763) = 124.8 kg/kmol
The results from Example 1 are given as a red X in the figures. The difference between molecular weight of naphtha from Eq (1) and (3) is 0.2 %.
Example 2: Molecular weight of a light gas oil from a distillation curve
D86 used to distille a gas oil sample showes:
10vol% recovered at 255 °C
30vol% recovered at 280 °C
50vol% recovered at 303 °C
70vol% recovered at 325 °C
90vol% recovered at 351 °C
The sample gravity is measured to be of 31.4°API
First, API gravity must be converted to specific gravity :
S, specific gravity = 141.5/(31.4°API +131.5) = 0.869
Then, VABP (volume average boiling point) and the distillation curve slope is calculated:
VABP = 0.2*(255+280+303+325+351) = 303 °C.
Slope = (351-255)/80 = 1.2 °C/% recovered.
MeABP can then be found by using correction factors :
MeABP = VABP + (-5)°C = 303-5 = 298°C
°C is then converted to K : MeABP = 298°C + 273 = 571 K
Finally, by applying equation (2) the molweight can be calculated:
Average MW = 1.6607E-04 * 571 2.1962 * 0.869 -1.0164 = 217 kg/kmol
Applying equation (4) gives
Average MW = 42.965 * 571 1.26007 * 0.869 4.98308 * e (2.097E-04*571-7.78712*0.869+2.08476E-03*571*0,869) = 232 kg/kmol
The difference between MW of gas oil from Eq (2) and (4) is 6.5 %.
Related Topics
-
Fluid Mechanics
The study of fluids - liquids and gases. Involving velocity, pressure, density and temperature as functions of space and time. -
Material Properties
Properties of gases, fluids and solids. Densities, specific heats, viscosities and more.
Related Documents
-
Alcohols and Carboxylic Acids - Physical Data
Molweight, melting and boiling point, density, pKa-values, as well as number of carbon and hydrogen atoms in molecules are given for 150 different alcohols and acids. -
API Gravity
API expresses the gravity or density of liquid petroleum products. Online API to Specific Gravity calculator. -
Crude Oil - Density vs. Temperature
Variations in crude oil density are shown as function of temperatur, together with volume correction factors. -
Density vs. Specific Weight and Specific Gravity
An introduction to density, specific weight and specific gravity. -
Fuel Oils - Densities vs. Temperature
Variations in fuel oils density as function of temperatur, together with volume correction factors. -
Hydrocarbon Mixtures - Average Boiling Points vs. Gravity and Molecular Weights
Formulas and examples of calculation of boiling point of hydrocarbon mixtures from gravity and molecular weight. -
Hydrocarbons - Physical Data
Molweight, melting and boiling point, density, flash point and autoignition temperature, as well as number of carbon and hydrogen atoms in each molecule for 200 different hydrocarbons. -
Hydrocarbons - Melting Point vs. Molecular Weight
Calculate melting point of hydrocarbons from molecular weight (molar mass). -
Jet Fuel - Density vs. Temperature
Variations in jet fuel density as function of temperatur, together with volume correction factors. -
Lubricating Oil - Densities vs. Temperature
Variations in lubricating oil density as function of temperatur, together with volume correction factors. -
Organic Nitrogen Compounds - Physical Data
Boiling and melting points of amines, diamines, pyrroles, pyridines, piperidines and quinolines shown together with their molecular structures, as well as molweights and density. -
Organic Sulfur Compounds - Physical Data
Boiling and melting points of thoils, sulfides, disulfides and thiophenes shown together with molecular structures, as well as molweights and density. -
Petroleum Products - Average Boiling Points
Definition, explanation and examples of calculation of various types of average boiling point of petroleum products and other mixtures of hydrocarbons: VABP, MABP, WABP, CABP and MeABP. -
Temperature
Introduction to temperature - including Celsius, Fahrenheit, Kelvin and Rankine definitions - and an online temperature converter.




