Propagation of Sound Indoors - the Room Constant
In a room the sound or noise will reach the receiver as direct and reverberant sound.
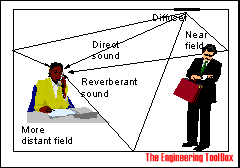
For a continuing sound source in a room the sound level is the sum of direct and reverberant sound. The sound pressure level for a receiver can be expressed as:
Lp = LN + 10 log(D / (4 π r2) + 4 / R) (1)
where
Lp = received sound pressure level (dB)
LN = sound power level from source (dB)
D = directivity coefficient (typical 1 for receivers in the middle of the room)
R = room constant (m2 Sabin)
π = 3.14 ....
r = distance from source (m)
Room Constant
The room constant express the acoustic property of a room.
R = A / (1- αm)
= ΣSi αi / (1- αm) (2)
where
R = room constant (m 2 Sabine)
A = total room sound absorption (m2 Sabine)
αm = mean absorption coefficient of the room
Si = individual surface area in the room (m2)
αi = absorption coefficient for individual surface in the room
Example - Received Sound
The sound power generated from a machine is 90 dB. The machine is located in a room with total sound aborption 12.2 m2 Sabine and mean absorption coefficient 0.2.
The room constant can be calculated as
R = (12.2 m2) / (1 - 0.2)
= 15.3 m2 Sabine
For a receiver located in the middle of the room with a directivity coefficient 1 and distance 2 m from the source - the received sound pressure level can calculated as
L p = (90 dB) + 10 log(1 / (4 π (2 m)2) + 4 / (15.3 m2 Sabine))
= 84.8 dB



