Manning's Formula and Gravity Flow
Calculate cross-sectional average velocity flow in open channels.
Manning's equation is an empirical equation that can be used to calculate cross-sectional average velocity flow in open channels
v = (k n / n) R h 2/3 S 1/2 (1)
where
v = cross-sectional mean velocity (ft/s, m/s)
k n = 1.486 for English units and k n = 1.0 for SI units
n = Manning coefficient of roughness - ranging from 0.01 (a clean and smooth channel) to 0.06 (a channel with stones and debris, 1/3 of vegetation)
R h = hydraulic radius (ft, m)
S = slope - or gradient - of pipe (ft/ft, m/m)
The Manning coefficients n in the English (Imperial) are equal to the coefficients in the SI system. The Manning coefficient is not dimensionless but the units are often omitted.
Units for (k n / n) in the SI system vs. the Imperial system can be expressed as:
(k n / n) = m 1/3 / s = 1.4859 ft 1/3 / s
Hydraulic radius can be expressed as
R h = A / P w (2)
where
A = cross sectional area of flow (ft2, m)
P w = wetted perimeter (ft, m)
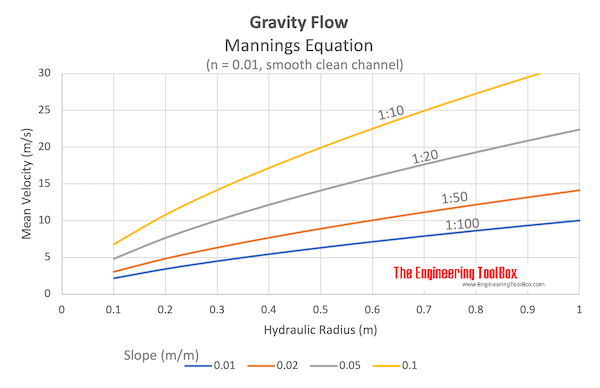
Download and print Gravity Flow - Mannings Equation Chart
The volume flow in the channel can be calculated as
q = A v = A (k n / n) R h 2/3 S 1/2 (3)
where
q = volume flow (ft3 /s, m3 /s)
A = cross-sectional area of flow (ft2, m2)
Example - Flow in an Open Channel
A channel with the shape of an half circle is 100% filled. The diameter of the half circle is 500 mm (0.5 m) and the channel is made of concrete with Manning coefficient 0.012 . The slope of the channel is 1/100 m/m .

make 3D models with the free Engineering ToolBox Sketchup Extension !
The cross section area of the half circle flow can be calculated as
A = (0.5 π ((0.5 m) / 2)2)
= 0.098 m2
The wetted perimeter of the half circle flow can be calculated as
P = 0.5 2 π (0.5 m) / 2)
= 0.785 m
The hydraulic radius of the channel can be calculated from (2) as
R h = A / P
= ( 0.098 m2> ) / ( 0.785 m )
= 0.125 m
The cross sectional mean velocity can be calculated from (1) as
v = (k n / n) R h 2/3 S 1/2
= (1.0 / 0.012) (0.125 m) 2/3 (1/100 m/m) 1/2
= 2.1 m/s
The volume flow can be calculated from (3) as
q = A v
= ( 0.098 m2) (2.1 m/s)
= 0.20 m3 /s
Gravity Flow Calculator - Half Filled Circular Pipe
The Gravity Flow Calculator is based on the equations and the example above above. It's valid for half filled circular pipe.
Related Topics
-
Flow Measurements
Flow metering principles - Orifice, Venturi, Flow Nozzles, Pitot Tubes, Target, Variable Area, Positive Displacement, Turbine, Vortex, Electromagnetic, Ultrasonic Doppler, Ultrasonic Time-of-travel, Mass Coriolis, Mass Thermal, Weir V-notch, Flume Parshall and Sluice Gate flow meters and more. -
Fluid Mechanics
The study of fluids - liquids and gases. Involving velocity, pressure, density and temperature as functions of space and time.
Related Documents
-
California Pipe Flow Metering Method
Calculate the discharge length from the open end of a partially filled horizontal pipe. -
Chezys Conduit Flow Equation
Calculating volume flow and velcity in open conduits. -
Flow Section Channels - Geometric Relationships
Geometric relationships like area, wetted perimeter and hydraulic diameter. -
Froude Number
Introduction to the Froude Number. -
Hazen-Williams Friction Loss Equation - calculating Head Loss in Water Pipes
Friction head loss (ftH2O per 100 ft pipe) in water pipes can be estimated with the empirical Hazen-Williams equation. -
Manning's Roughness Coefficients
Manning's roughness coefficients for some common materials. -
Piping Equations
Calculate cross-sectional areas, weight of empty pipes, weight of pipes filled with water, inside and outside surface areas. -
Rainfall on Roofs and Gutter Slopes
Draining of roof areas and recommended gutter slopes -
Sewage Sludge - Viscosities
Viscosity of sewage sludge vs. content of solids. -
Sewer Pipes - Capacities vs. Slope
Carrying capacities of sewer and wastewater pipes - gpm and liter per second. -
Storm-Water Conductors
Roof drain capacities. -
Storm-Water Runoff Coefficients vs. Surface
Storm-water runoff coefficients for various surfaces -
Surface Roughness vs. Mechanical Processing
Mechanical production methods and their surface roughness. -
Volume Flow - Online Unit Converter
Convert between volume flow units like gpm, liter/sec, cfm, m3/h.




