Levers

A lever is a mechanism that can be used to exert a large force over a small distance at one end of the lever by exerting a small force over a greater distance at the other end.

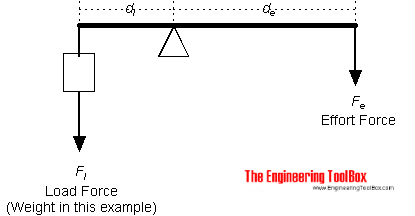
The moment action on both sides of the lever is equal and can be expressed as

F_e d_e = F_l d_l                             (1)

where

F_e = effort force (N, lb)

F_l = load force (N, lb) (note that weight is a force)

d_l = distance from load force to fulcrum (m, ft)

d_e = distance from effort force to fulcrum (m, ft)

The effort force can be calculated by modifying (1) to

F_e = F_l d_l / d_e       

    = m a_g d_l / d_e                        (1b)

where

m = mass (kg, slugs)

a_g = acceleration of gravity (9.81 m/s², 32.17 ft/s²)

Lever Calculator

This calculator can used to calculate lever effort force. It can be used for both metric and imperial units as long as the use of units are consistent.

F_l - load force (N, kg, lb)

d_l - distance form load force to fulcrum (m, ft)

d_e - distance from effort force to fulcrum (m, ft)

• note that kg is the SI units for mass - more about mass and weight (force)

Example - Improvised Car Lift

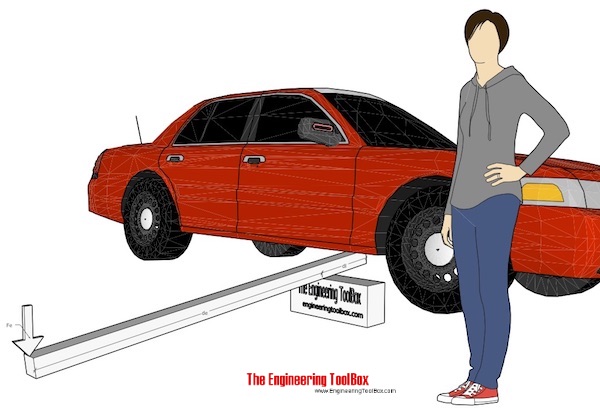
An improvised car lift can be made with a piece of lumber as illustrated in the figure above. With distance load to fulcrum 0.2 m, distance effort force to fulcrum 2 m and a load on the lever - half the weight of the car 2000 kg - the effort force can be calculated

F_e = (0.5 2000 kg) (9.81 m/s²) (0.2 m) / (2 m)

    = 981 N

    ≈ 100 kg 

Orders of Levers

First-order levers

• the fulcrum is positioned between the effort and the load
• the effort is smaller than the load
• the effort moves further than the load
• the lever can be considered as a force magnifier

Second-order Levers

• the effort and the load are positioned on the same side of the fulcrum but applied in opposite directions
• the load lies between the effort and the fulcrum
• the effort is smaller than the load
• the effort moves further than the load
• the lever can be considered as a force magnifier

Third-order Levers

• the effort lies between the load and the fulcrum
• the effort is greater than the load
• the load moves further than the effort
• the lever can be considered as a distance magnifier

Example - First-Class (Order) Lever - A force (weight) of 1 pound is exerted at the end of a lever at distance 1 ft from the fulcrum

The effort force at a distance of 2 ft from the fulcrum can be calculated as

F_e = (1 lb) (1 ft) / (2 ft)

    = 0.5 (lb)

The formula (1) can be modified to express required load if you know the effort, or required distance from fulcrum if load and effort forces are known and so on.

The level above where the fulcrum located between the load and effort force is often characterized as a first-class level mechanism.

A level where the load and effort force are located on the same side of the fulcrum is often characterized as a second-class level mechanism.

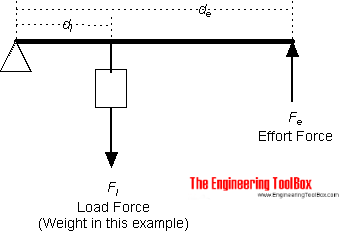
Example - Second-Class (Order) Lever

A force (weight) of 1 pound is exerted at a distance of 1 ft from the fulcrum.

The effort force at a distance of 2 ft from the fulcrum can be calculated as

F_e = (1 lb) (1 (ft) / (2 ft)

    = 0.5 (lb)

Example - Lever calculation with SI-units - weight of 1 kg mass acting 1 m from the fulcrum

The effort force at a distance of 2 m from the fulcrum can be calculated as

F_e = (1 kg) (9.81 m/s²) (1 m) / (2 m)

    = 4.9 N

A lever mechanism where the input effort is higher than than the output load is often characterized as a third-class lever mechanism.

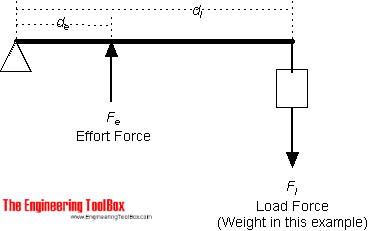
Example - Third-Class (Order) Lever

A force (weight) of 1 pound is exerted at a distance of 2 ft from the fulcrum.

The effort force at a distance of 1 ft from the fulcrum can be calculated as

F_e = F_l d_l / d_e

    = (1 lb) (2 ft) / (1 ft)

    = 2 (lb)

One or more forces acting on a lever

A lever with two acting load forces and one effort force is indicated in the sketch below:

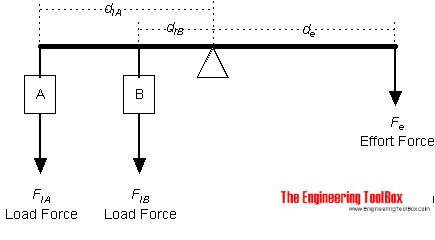
The generic equation for one effort force with one or more acting load forces can be expressed as

F_e = (F_lA d_lA +  F_lB d_lB +.. + F_lN d_lN) / d_e                                                (2)

This equation is modified for three acting loads below.

Example - A Lever with three acting loads and one effort force

A weight A of 1 pound is exerted at a distance of 1 ft from the fulcrum. A weight B of 2 pound is exerted at a distance of 2 ft from the fulcrum, and a weight C of 3 pound is exerted at a distance of 3 ft from the fulcrum.

The effort force at a distance of 2 ft from the fulcrum can be calculated as

F_e = (F_lA d_lA +  F_lB  d_lB +F_lC d_lC) / d_e

    = ((1 lb) (1 ft) + (2 lb) (2 ft) + (3 lb) (3 ft)) / (2 ft)

    = 7 (lb)