Decibel
Logarithmic unit used to describe ratios of signal levels - like power or intensity - to a reference level.
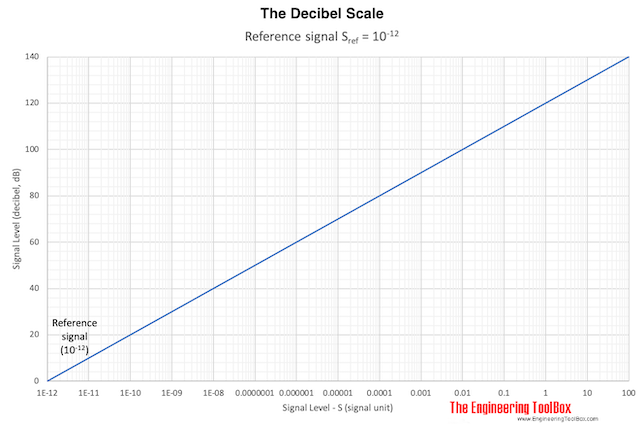
The decibel is a logarithmic unit used to describe the ratio of a signal level - like power, intensity or amplitude - to a reference level.
- the decibel express the level of a value relative to a reference value
Two types of decibel are normally used:
- for power ratios - dB is defined as ten times the logarithm in base 10
- for amplitude ratios - root power quantities - a change in amplitude by a factor of 10 corresponds to 20 dB change in level
Decibel Definition - Power Ratios
The decibel level of a signal can be expressed as
L = 10 log (S / S ref) (1)
where
L = signal level (decibel, dB)
S = signal - intensity or power level (signal unit)
S ref = reference signal - intensity or power level (signal unit)
Decibel is a dimensionless value of relative ratios. The signal units depends on the nature of the signal - can be W for power.
A decibel is one-tenth of a Bel - named after Alexander Graham Bell, the inventor of the telephone.
Note! - the decibel value of a signal increases with 3 dB if the signal is doubled (L = 10 log (2) = 3).
| dB | Power Ratio (S/Sref) | Amplitude Ratio (A/Aref) |
|---|---|---|
| -40 | 0.0001 | 0.01 |
| -20 | 0.01 | 0.1 |
| 0 | 1 | 1 |
| 3 | 2 | √2 |
| 6 | 4 | 2 |
| 10 | 10 | 3.162 |
| 20 | 100 | 10 |
If the decibel value and reference level are known the absolute signal level can be calculated by transforming (1) to
S = S ref 10 (L / 10) (2)
Decibel Calculator
Example - Lowest Hearable Sound Power
10 -12 W is normally the lowest sound power possible to hear and this value is normally used as the reference power in sound power calculations.
The sound power in decibel from a source with the lowest sound hearable can be calculated as
L = 10 log ( (10 -12 W ) / (10 -12 W ))
= 0 dB
Example - Highest Hearable Sound Power
100 W is almost the highest sound power possible to hear. The sound power in decibel from a source with the highest possible to hear sound power can be calculated as
L = 10 log ( (100 W) / (10 -12 W ))
= 140 dB
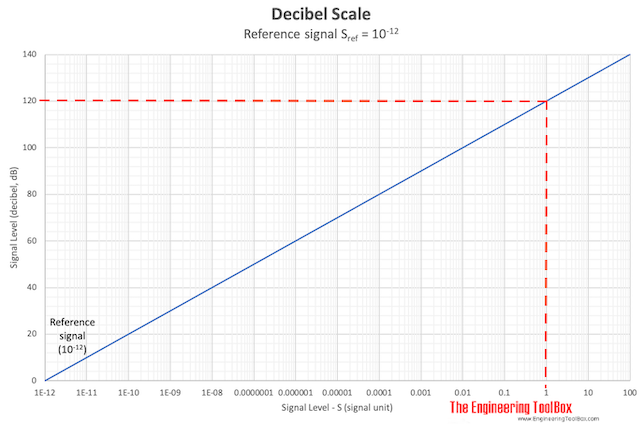
Example - Sound Power from a Fan
A fan creates 1 W of sound power. The noise level from the fan in decibel can be calculated as
L = 10 log ((1 W) / (10 -12 W ))
= 120 dB
Example - Sound Intensity and Decibel
The difference in decibel between sound intensity 10 -8 W/m 2 and sound intensity 10 -4 W/m 2 ( 10000 units) can be calculated as
ΔL = 10 log ((10 -4 W/m 2) / (10 -12 W/m 2)) - 10 log ((10 -8 W/m 2) / (10 -12 W/m 2))
= 40 dB
Increasing the sound intensity by a factor of
- 10 raises its level by 10 dB
- 100 raises its level by 20 dB
- 1000 raises its level by 30 dB
- 10000 raises its level by 40 dB and so on
Decibel Ratios - Amplitude Ratios
L = 20 log (A / A ref) (3)
where
L = signal level (decibel, dB)
A = amplitude level (signal unit)
A ref = amplitude level level (signal unit)
Related Topics
-
Acoustics
Room acoustics and acoustic properties. decibel A, B and C calculations. Noise Rating (NR) curves. Sound transmission through walls. Calculate sound pressure, sound intensity and sound attenuation. -
Miscellaneous
Engineering related topics like Beaufort Wind Scale, CE-marking, drawing standards and more. -
Noise and Attenuation
Noise is usually defined as unwanted sound - noise, noise generation, silencers and attenuation in HVAC systems.
Related Documents
-
Decibel A, B and C
Sound pressure filters that compensates for the hearing sensed by the human ear. -
Logarithms
The rules of logarithms - log10 and loge for numbers ranging 1 to 1000. -
Maximum Sound Pressure Levels in Rooms
Maximum recommended sound pressure levels in rooms like kindergartens, auditoriums, libraries, cinemas and more. -
Noise generated in Air Ducts
Estimate noise generated by air flow in ducts. -
Outdoor Ambient Sound Pressure Levels
Outdoor ambient sound pressure levels (dBA) in rural and urban business and industrial environments with or without limited traffic. -
Phonetic Alphabet
The phonetic alphabet used in international aircraft communications. -
Scales of Objects
The relative scale of objects. -
Signals - Adding Decibels
The logarithmic decibel scale is convenient when adding signal values like sound power, pressure and others from two or more sources. -
SIL - the Speech Interference Levels
Background noise frequencies that interferes with speech. -
Sound Intensity
Acoustic power of sound per unit area. -
Sound Intensity, Power and Pressure Levels
Introduction to decibel, sound power, intensity and pressure. -
Sound Pressure
Sound Pressure is the force of sound on a surface perpendicular to the propagation of sound. -
Use of Telephones in Noisy Areas
Satisfactory, difficult and impossible noise levels for telephone use in noisy areas.