Cable Loads
Force and tension in cables with uniform loads.

The equations below can also be used for cables only loaded with their own weight as long as the sagging height (h) vs. length (L) ratio is below 0.1.
Uniformly Loaded Cables with Horizontal Loads
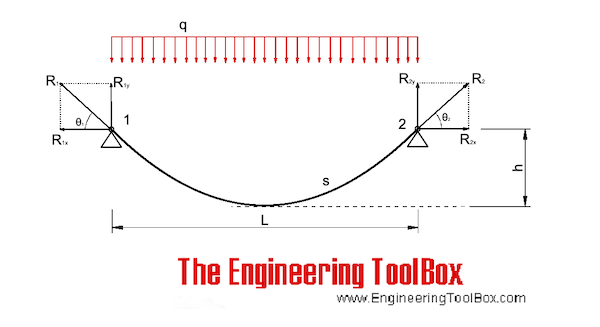
The cable follows the shape of a parable and the horizontal support forces can be calculated as
R1x = R2x
= q L2 / (8 h) (1)
where
R1x = R2x = horizontal support forces (lb, N) (equal to midspan lowest point tension in cable)
q = unit load (weight) on the cable (lb/ft, N/m)
L = cable span (ft, m)
h = cable sag (ft, m)
The vertical support forces at the end of the cable can be calculated as
R1y = R2y
= q L / 2 (1a)
where
R1y = R2y = vertical support forces (lb, N)
The resultant forces acting in the end supports - and in the direction of the cable close to the supports - can be calculated as
R1 = R2
= (R1x2 + R1y2)0.5
= (R2x2 + R2y2)0.5 (1b)
where
R1,2 = resultant force at the support (lb, N)
The angle θ can be calculated as
θ = tan-1(R1y / R1x)
= tan-1(R2y / R2x) (1c)
The length of the sagged cable can be approximated to
s = L + 8 h2 / (3 L) (1d)
where
s = cable length (ft, m)
Note that the equation is not valid when h > L / 4.
- kip = 1000 lb
- klf = kip per linear foot
Uniformly Loaded Cables with Horizontal Loads - Calculator
R12x (N, lb): 45
R12y (N, lb): 60
R12 (N, lb): 75
θ (degrees): 53.1
s (m, ft):
Example - Uniform Cable Load, Imperial units
A cable with length 100 ft and a sag 30 ft has a uniform load 850 lb/ft. The horizontal supports and mid-span cable forces can be calculated as
R1x = R2x
= (850 lb/ft) (100 ft)2 / (8 (30 ft))
= 35417 lb
The vertical forces at the supports can be calculated as
R1y = R2y
= (850 lb/ft) (100 ft) / 2
= 42500 lb
The resultant forces acting in the supports can be calculated as
R1,2 = ((35417 lb)2 + (42500 lb)2)0.5
= 55323 lb
The angle θ can be calculated as
θ = tan-1((42500 lb) / (35417 lb))
= 50.2 o
The length of the sagged cable can be approximated to
s = (100 ft) + 8 (30 ft)2 / (3 (100 ft))
= 124 ft
Example - Uniform Cable Load, SI units
A cable with length 30 m and a sag 10 m has a uniform load of 4 kN/m. The horizontal supports and mid-span cable forces can be calculated as
R1x = R2x
= (4000 N/m) (30 m)2 / (8 (10 m))
= 45000 N
= 45 kN
The vertical support forces can be calculated as
R1y = R2y
= (4000 N/m) (30 m) / 2
= 60000 N
= 60 kN
The angle θ can be calculated as
θ = tan-1((60 kN) / (45 kN))
= 53.1 o
The resultant force acting in the supports can be calculated as
R1,2 = ((45000 N)2 + (60000 N)2)0.5
= 75000 N
= 75 kN
The length of the sagged cable can be approximated to
s = (30 m) + 8 (10 m)2 / (3 (30 m))
= 38.9 m
Example - Known Tension at the Supports - Calculate Sagging and Length of Cable
For a 30 m long cable with uniform load 4 kN/m the resulting tension in the cable at the end supports are 100 kN.
The vertical forces in the supports can be calculated as
R1y = R2y
= (4 kN/m) (30 m) / 2
= 60 kN
The horizontal forces in the supports can be calculated as
R1x = R2x
= ((100 kN)2 - (60 kN)2)0.5
= 80 kN
The angle θ can be calculated as
θ = tan-1((60 kN) / (80 kN))
= 36.9 o
The sagging can be calculated by modifying eq.1 to
h = q L2 / (8 R1x)
= (4 kN/m) (30 m)2 / (8 (80 kN))
= 5.6 m
The length of the sagged cable can be estimated to
s = (30 m) + 8 (5.6 m)2 / (3 (30 m))
= 32.8 m
Uniformly Loaded Cables with Inclined Chords
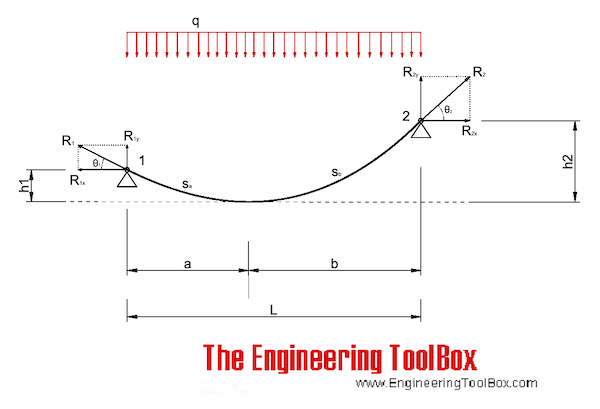
Inclined Cable Calculator - with Uniform Horizontal Loads
The calculator below can be used for cables with inclined chords and uniformly loads. The calculator is based on an iterative algorithm where the parable shaped cable is adapted to span L, height h1 and h2 according the figure above. The parable equation estimated below can be used to replicate the shape in spreadsheets or CAD systems.
The horizontal support forces in x-direction can be calculated as
R1x = R2x
= q a2 / (2 h1)
= q b2 / (2 h2) (2a)
If b > a the maximum forces in the cable and at support 1 and 2 can be calculated as
R2 = (R2x2 + (q b)2)0.5 (2c)
R1 = (R1x2 + (q a)2)0.5 (2d)
- and the vertical forces at support 1 and 2 can be calculated as
R2y = (R22 - R2x2)0.5 (2e)
R1y = (R12 - R1x2)0.5 (2f)
The angles between the horizontal and resulting forces can be calculated as
θ2 = cos-1(R2x / R2) (2g)
θ1 = cos-1(R1x / R1) (2g)
The length of the sagged cable can be estimated as
sb = b (1 + 2/3 (h2 / b)2) (2h)
sa = a (1 + 2/3 (h1 / a)2) (2i)
s = sa + sb (2j)
Example - Inclined Cable with Uniform Load, SI units
A cable with span 30 m, length a = 7.2 m, length b = 22.8 m, sag h1= 1 m and sag h2 = 10 m has a uniform load of 4 kN/m.
The horizontal support forces can be calculated as
R1x = R2x
= (4 kN/m) (30 m)2 / (2 (((1 m))0.5 + ((10 m))0.5))
= 104 kN
The resulting support forces can be calculated as
R2 = ((103.9 kN)2 + ((4 kN/m) (22.8 m))2)0.5
= 138 kN
R1 = ((103.9 kN)2 + ((4 kN/m) (7.2 m))2)0.5
= 108 kN
The vertical forces in the supports can be calculated as
R2y = ((138.2 kN)2 - (103.9 kN)2)0.5
= 91.2 kN
R1y = ((107.8 kN)2 - (103.9 kN)2)0.5
= 28.8 kN
The angles between resulting and horizontal forces in support 1 and 2 can be calculated as
θ2 = cos-1((103.9 kN)/ (138.2 kN))
= 41.3 o
θ1 = cos-1((103.9 kN)/ (107.8 kN))
= 15.5 o
The length of the sagged cable can be calculated as
sb = (22.8 m) (1 + 2/3 ((10 m) / (22.8 m))2)
= 25.7 m
sa = (7.2 m) (1 + 2/3 ((1 m) / (7.2 m))2)
= 7.3 m
s = (7.3 m) + (25.7 m )
= 33 m
Related Topics
-
Mechanics
The relationships between forces, acceleration, displacement, vectors, motion, momentum, energy of objects and more. -
Statics
Forces acting on bodies at rest under equilibrium conditions - loads, forces and torque, beams and columns.
Related Documents
-
Forces and Tensions in Ropes due to Angle
Reduced load capacities in ropes, cables or lines - due to acting angle. -
Manila Ropes - Strength
Minimum breaking strength and safe load of manila 3-strand rope. -
Polyester Polyolefin Ropes - Strengths
Polyester Polyolefin dual fiber 3-strand rope - minimum breaking strength and safe load. -
Polyester Ropes - Strengths
Polyester 3-strand and 8-strand rope - minimum breaking strength and safe load. -
Polypropylene Fiber Ropes - Strengths
Polypropylene fiber 3-strand and 8 strand rope - minimum breaking strength and safe load. -
Shackles - Safe Loads
Safe loads of shackles. -
Sisal Ropes - Strengths
Sisal rope 3-strand, minimum breaking strength and safe load. -
Wire Rope Slings
Sling angles and influence on capacity.




