Conservation of Mass
The Law of Conservation of Mass states that mass can neither be created or destroyed.
The Law of Mass Conservation states that
"mass can neither be created nor destroyed"
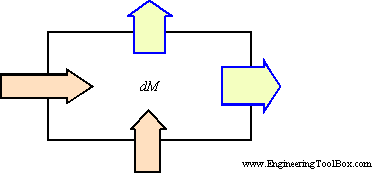
The inflows, outflows and change in storage of mass in a system must be in balance.
The mass flow in and out of a control volume (through a physical or virtual boundary) can for an limited increment of time be expressed as:
dM = ρi vi Ai dt - ρo vo Ao dt (1)
where
dM = change of storage mass in the system (kg)
ρ = density (kg/m3)
v = speed (m/s)
A = area (m2)
dt = an increment of time (s)
If the outflow is higher than the inflow - the change of mass dM is negative -
- the mass of the system decreases
And obvious - the mass in a system increase if the inflow is higher than the outflow.
The Law of Mass Conservation is fundamental in fluid mechanics and a basis for the Equation of Continuity and the Bernoulli Equation.
Example - Law of Mass Conservation
Water with density 1000 kg/m3 flows into a tank through a pipe with inside diameter 50 mm. The velocity of the fluid in the pipe is 2 m/s. The water flows out of the tank through a pipe with inside diameter 30 mm with a velocity of 2.5 m/s.
Using equation (1) the change in the tank content after 20 minutes can calculated as:
dM = (1000 kg/m3) (2 m/s) (3.14 (0.05 m)2/ 4) ((20 min) (60 s/min))
- (1000 kg/m3) (2.5 m/s) (3.14 (0.03 m)2/ 4) ((20 min) (60 s/min))
= 2591 kg
Related Topics
-
Fluid Mechanics
The study of fluids - liquids and gases. Involving velocity, pressure, density and temperature as functions of space and time.
Related Documents
-
Equations in Fluid Mechanics
Equations used in fluid mechanics - like Bernoulli, conservation of energy, conservation of mass, pressure, Navier-Stokes, ideal gas law, Euler equations, Laplace equations, Darcy-Weisbach Equation and more. -
Fluid Flow - Equation of Continuity
The Equation of Continuity is a statement of mass conservation. -
Technical Terms in Fluid Mechanics
Some commonly used technical terms in fluid mechanics.




