Pendulum
A simple pendulum oscillates in the vertical plane due to gravity.
A simple - or mathematical - pendulum consists of a rigid body suspended from a fixed horizontal axis about which the body may oscillate in a vertical plane due to the action of gravity.
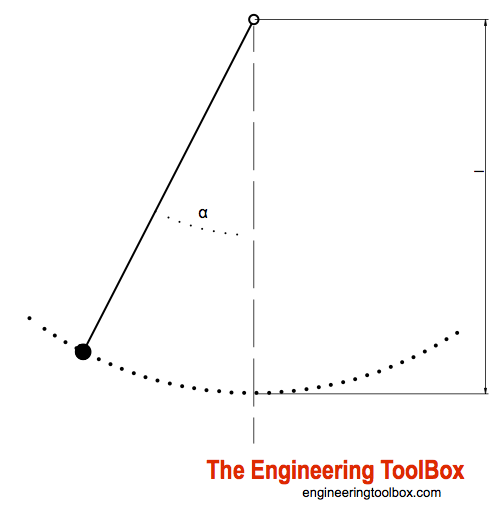
The oscillating period for a simple pendulum can be calculated as
T = 2 π (l / ag)1/2 (1)
where
T = oscillating period for one cycle (s)
l = length of the pendulum (m, ft)
ag = acceleration of gravity (9.81 m/s2, 32.17 ft/s2)
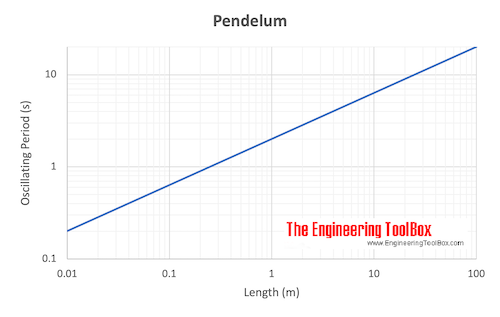
Example - Calculate the length of a pendulum with an oscillating period of 1 sec, 10 sec and 100 sec
The length of a pendulum with a given oscillating period can be calculated by transforming (1) to:
l = (T / (2 π))2 ag
Length for 1 sec - typically for an old fashion pendulum clock:
l = ((1 s) / (2 π))2 (9.81 m/s2)
= 0.249 (m)
Pendulum clocks were the world standard for accurate timekeeping for 270 years until the quartz clock was invented in 1927.
Length for 10 sec:
l = ((10 s) / (2 π))2 (9.81 m/s2)
= 24.9 (m)
Length for 100 sec:
l = ((100 s) / (2 π))2 (9.81 m/s2)
= 2487 (m)
Four Types Of Pendulums
It is common to differentiate between four types of pendulums:
- Compound or Physical Pendulum - A rigid body suspended from a fixed horizontal axis. The body may oscillate in a vertical plane due to the action of gravity.
- Simple or Mathematical Pendulum - Similar to the compound or physical pendulum but the mass is concentrated in a single point and oscillates back and forth in the vertical plane. The mass point is connected to a horizontal axis with a weightless chord.
- Conical Pendulum - Similar to the simple pendulum except that the weight suspended by the chord moves in uniform speed around the circumference of a circle in the horizontal plane.
- Torsional Pendulum - A disk fixed to a slender rod. The rod is fastened to a fixed frame. If the disk is twisted it will oscillate back and forth about the axis of the rod.
Related Topics
-
Dynamics
Motion - velocity and acceleration, forces and torque.
Related Documents
-
Harmonic Oscillator
A simple harmonic oscillator.
