Continuous Beams - Moment and Reaction Support Forces
Moments and reaction support forces with distributed or point loads.
Continuous Beam with Distributed Load
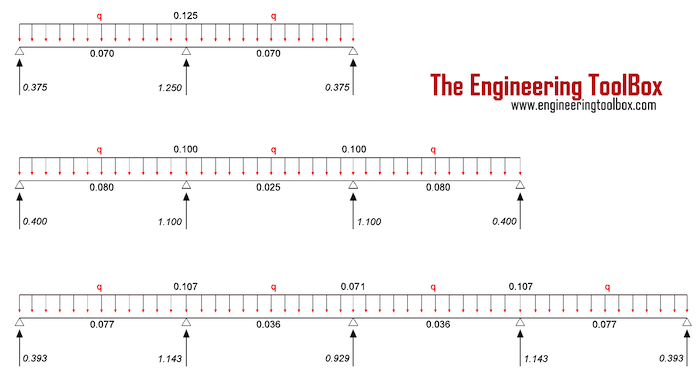
For a continuous beam with 3, 4 or 5 supports and distributed load the reaction support forces can be calculated as
R = cr q L (1)
where
R = reaction support force (N, lbf)
cr = reaction support force coefficient from the figure above
q = distributed load (N/m, lbf/ft)
L = span length (m, ft)
The moments can be calculated as
M = cm q L2 (2)
where
M = beam moment (Nm, lbf ft)
cm = moment coefficient from the figure above
Example - Continuous Beam with Distributed Load
The reaction forces in the end supports for a continuous beam with 3 supports and distributed load 1000 N/m can be calculated as
Rend = (0.375) (1000 N/m)
= 375 N
= 0.38 kN
The reaction force in the center support can be calculated as
Rcenter = (1.250) (1000 N/m)
= 1250 N
= 1.25 kN
The beam moments at the middle of spans with span length 1m can be calculated as
Mend = (0.070) (1000 N/m) (1 m)2
= 70 Nm
The beam moment at the center support can be calculated as
Mcenter = (0.125) (1000 N/m) (1 m)2
= 125 Nm
Continuous Beam with Point Loads
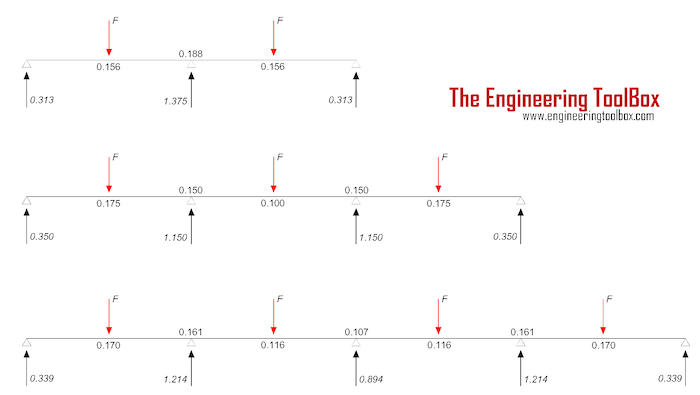
For a continuous beam with 3, 4 or 5 supports and point loads the reaction support forces can be calculated as
R = cr F (3)
where
cr = reaction support force coefficient from the figure above
F = point load (N, lbf)
The moments can be calculated as
M = cm F L (4)
where
cm = moment coefficient from the figure above
Example - Continuous Beam with Point Loads
The reaction forces in the end supports for a continuous beam with 3 supports and 2 point loads 1000 N can be calculated as
Rend = (0.313) (1000 N)
= 313 N
= 0.31 kN
The reaction force in the center support can be calculated as
Rcenter = (1.375) (1000 N)
= 1375 N
= 1.4 kN
The beam moments at point loads with span length 1m can be calculated as
Mend = (0.156) (1000 N) (1 m)
= 156 Nm
The beam moment at the center support can be calculated as
Mcenter = (0.188) (1000 N) (1 m)
= 188 Nm
Related Topics
-
Beams and Columns
Deflection and stress in beams and columns, moment of inertia, section modulus and technical information.
Related Documents
-
Beam Loads - Support Force Calculator
Calculate beam load and supporting forces. -
Beams - Fixed at Both Ends - Continuous and Point Loads
Stress, deflections and supporting loads. -
Beams - Fixed at One End and Supported at the Other - Continuous and Point Loads
Supporting loads, moments and deflections. -
Beams - Supported at Both Ends - Continuous and Point Loads
Supporting loads, stress and deflections. -
British Universal Columns and Beams
Properties of British Universal Steel Columns and Beams. -
Cantilever Beams - Moments and Deflections
Maximum reaction forces, deflections and moments - single and uniform loads. -
Drawbridge - Force and Moment vs. Elevation
Calculate the acting forces and moments when elevating drawbridges or beams. -
HE-A Steel Beams
Properties of HE-A profiled steel beams. -
HE-B Steel Beams
Properties of HE-B profiled steel beams. -
Three-Hinged Arches - Continuous and Point Loads
Support reactions and bending moments. -
Wood Beams - Strength of Material
Bending and compression strength of wood species used in beams.




