Bollard Forces
Friction, load and effort forces acting in ropes turned around bollards.
Bollards are common on quays and used to moore ships and boats. By turning a rope around a pole the effort force required to hold the load force can be reduced dramatically.
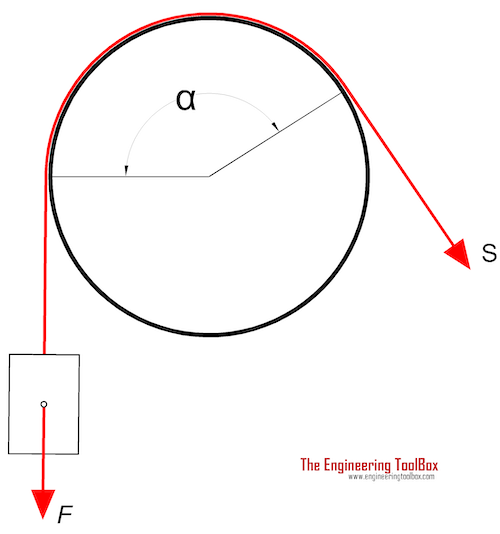
The effort force in a rope around a bollard can be calculated as
S = F e-(μ αrad ) (1)
where
S = effort force in the rope (N, lb)
F = load force (N, lbf)
e = 2.718..
μ = friction coefficient (approximately 0.3 - 0.5 is common for a rope around a steel or cast iron bollard)
αrad = 2 π αdegrees / 360 = angle where the rope is in contact with the bollard (radians)
αdegrees = angle where the rope is in contact with the bollard (degrees)
Angle - turns, degrees and radians
- 1/4 turn : 90 degrees => α = 1/2 π
- 1/2 turn : 180 degrees => α = π
- 1 turn : 360 degrees => α = 2 π
- 2 turns : 720 degrees => α = 4 π
Example - A rope with One turn around a Bollard
One turn equals to 360 degrees or 2 π radians. With a friction coefficient of 0.5 the effort force in the rope can be calculated as
S = F e-(0.5 2 π)
= 0.043 F (N)
One turn around the bollard reduces the required effort force to less than 5% of the load force.
Example - Shoring a ship
The retardation (negative acceleration) of a ship arriving at quay with velocity 0.05 m/s and stopped within 2 seconds - can be calculated as
a = dv / dt (2)
= (0.05 m/s) / (2 s)
= 0.025 (m/s2)
With ship mass 20000 kg the required force in the rope from the ship (load) can be calculated as
F = m a (3)
= (20000 kg) (0.025 m/s2)
= 500 N
= 0.5 kN
The required effort force in the rope with a half turn around the bollard ( 180 degrees or π radians) with a friction coefficient of 0.4 can be calculated as
S = (500 N) e-0.4 π
= 142 N
= 0.14 kN
The Effort Force - Load Force ratio for various rope angles are indicated in the chart below:
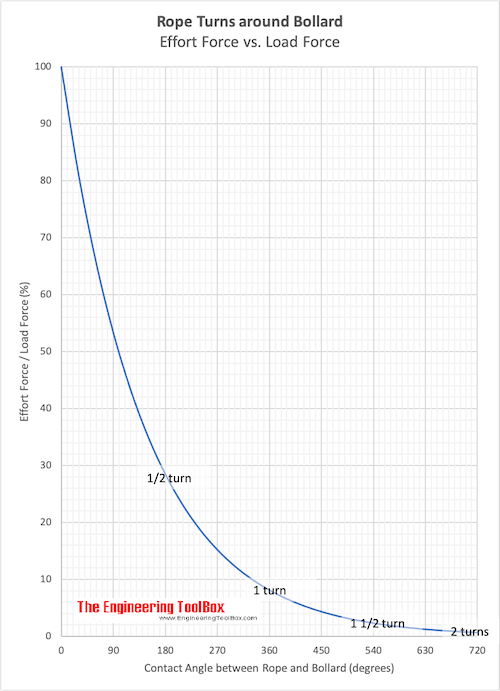
Download and print Rope Turns around Bollard Effort Force vs. Load Force Chart
- friction coefficient 0.5
Bollard (or Pole) Effort Force Calculator
This calculator is based on the equation above and can be used to calculate the effort force in ropes turned around poles or bollards. Note that the calculator uses degrees for the turns.
