Gear Trains - Bicycle Gearing Calculator
Gear train transmissions - bicycle gearing.
A simple gear can change magnitude and line of action of an effort force.
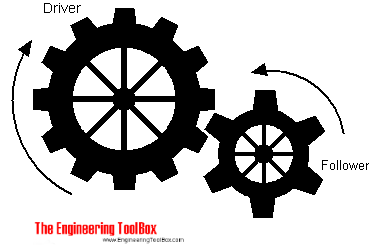
The effort force is applied to the "driver" and the load is applied to the "follower" .
Transmission - or Movement - Ratio
Transmission - or movement - ratio can be expressed as
M = n D / n F = t F / t D (1)
where
i M = movement ratio
n D = revolutions of driver (rpm)
n F = revolutions of follower (rpm)
t F = number of teeth on follower
t D = number of teeth on driver
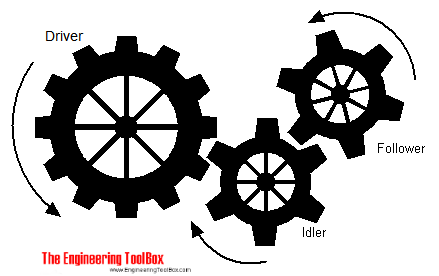
When the same direction of rotation is required for the driver and the follower, an idler wheel is used.
Gear Calculator
Calculate follower revolutions.
The movement ratio for a gear with an idler wheel can be expressed as
i M = n D / n F = (t I / t D ) (t F / t I ) = t F / t D (1b)
where
t I = number of teeth on idler
Moment Ratio
The moment - or torque - ratio for a transmission can be expressed as
i T = M F / M L = 1 / (i M μ) (2)
where
i T = moment ratio
μ = transmission efficiency
M L = output moment of load from follower (Nm, lb ft)
M F = input moment of force on driver (Nm, lb ft)
Transmission - Moment Ratio Calculator
Calculate follower output moment load.
The calculator is generic and can be used for SI and Imperial units - output units equals input units.
Make 3D models of spurs and gears with the Engineering ToolBox SketchUp plugin
 Spurs and Gears - Use the awesome SketchUp to make 3D models of spurs and gears
Spurs and Gears - Use the awesome SketchUp to make 3D models of spurs and gears
Typical Gear Ratios
Typical gear ratios for different types of gear sets are indicated below.
| Type of Gear set | Typical Gear Ratios | |
|---|---|---|
| Min | Max | |
| Spur gear, external | 1 : 1 | 5 : 1 |
| Spur gear, internal | 1.5 : 1 | 7 : 1 |
| Helical gear, external | 1 : 1 | 10 : 1 |
| Helical gear, internal | 1.5 : 1 | 10 : 1 |
| Straight bevel gear | 1 : 1 | 8 : 1 |
| Spiral bevel gear | 1 : 1 | 8 : 1 |
| Epicyclic planetary gear | 3 : 1 | 12 : 1 |
| Epicyclic star gear | 2 : 1 | 11 : 1 |
Bicycle Gearing
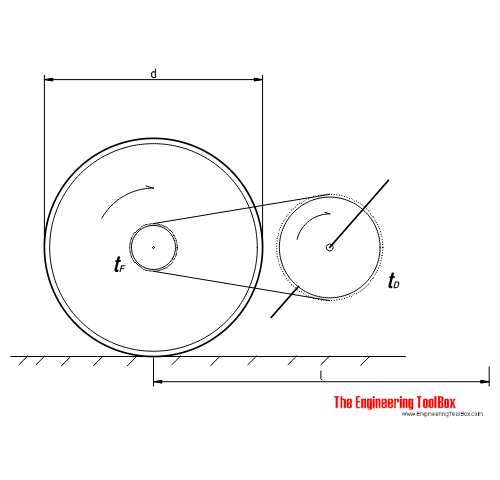
The revolutions of a bicycle wheel when pedaling can be calculated by transforming (2) :
n F = n D t D / t F (3)
where
n F = revolutions of the bicycle wheel (rpm)
n D = revolutions of the pedaling (rpm)
t D = number of teeth in the pedaling sprocket
t F = number of teeth in wheel sprocket
The distance traveled by the wheel can be calculated by multiplying wheel revolutions with wheel circumference:
l = c n F
= c n D t D / t F
= π d n D t D / t F (3b)
where
l = outer wheel traveled length or distance (m, in)
c = outer wheel circumference (m, in)
d = outer wheel diameter (m, in)
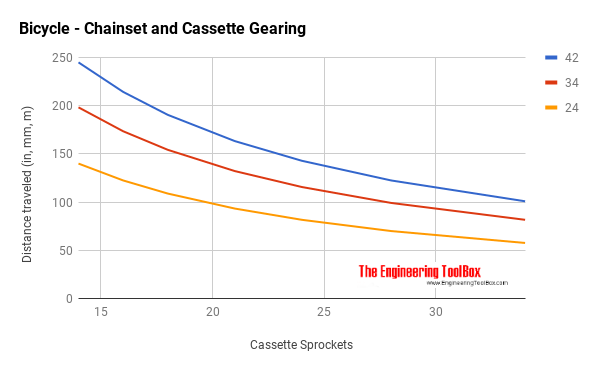
Example - Bicycle Gear
A mountain bike with 26 inch outer diameter wheels has a 42/34/24T chain-set and a 7-speed 14-34 cassette in the rear wheel.
The outer circumference of the wheel can be calculated as
c = π (26 in)
= 81.7 in
The distance traveled by the wheel in the lowest gear - for one pedaling revolution - using the smallest sprocket in the chainset (24T) and the largest sprocket in the cassette (34T) - can be calculated using (3b) as
l = (1) (81.6 in) (24) / (34)
= 57.7 in
The distance traveled by the wheel in the highest gear - for one pedaling revolution - using the largest sprocket in the chainset (42T) and the smallest sprocket in the cassette (14T) - can be calculated as
l = (1) (81.6 in) (42) / (14)
= 244.8 in
Bicycle Gearing Calculator
Calculate distance traveled by wheel.
The calculator is generic and can be used for SI and Imperial units - output units equals input units.
Bicycle Gearing Calculator - Template
Make your own graphical Bicycle Gearing Calculator by using this Google Docs template!
Related Topics
-
Mechanics
The relationships between forces, acceleration, displacement, vectors, motion, momentum, energy of objects and more.
Related Documents
-
Belt Transmissions - Speed and Length of Belts
Calculate length and speed of belt and belt gearing. -
Belts - Power Transmission and Efficiency
Calculate belts power transmission and efficiency -
Belts - Pulley Diameters vs. Speed
The pulley laws - driver and driven - diameter and rpm -
Efficiency of Small Machine Elements
Friction and efficiency in bearings and roller chains. -
Gear Reducing Formulas
Output torque, speed and horsepower with gears. -
Gears
Gears effort force vs. load force.